2027: Lightning Distance
Explanation[edit]
The usual trick for determining the distance to a lightning flash is to count the seconds from when you see the flash until when you hear thunder, and divide by five to get miles (or three to get kilometers). This works because the transmission of light is essentially instantaneous over the relevant distances, while the speed of sound is 331.2 m/s (1,087 ft/s, 1,192 km/h, or 741 mph, varying a bit based on temperature), or about 1/5 mile per second (1/3 kilometer per second).
This comic subverts the usual trick by having Megan describe a highly impractical alternative method. Megan's method is based on the fact that the speed of electromagnetic radiation, which includes light and radio waves, is not truly fixed and varies by wavelength in a refractive medium (consider the classic case of visible light in a prism). The electromagnetic radiation emitted by lightning on Earth also has to travel through air, which changes its speed in a fashion which depends on its frequency.
Lightning is most visibly observable in the near-infrared visible spectrum around a wavelength of 777 nm. The refractive index (n) of air at 15˚C for a wavelength of 777 nm is 1.0002752, which equates to a speed of light of 299,709,978 m/s given the relation n=c/v, where c=speed of light in a vacuum and v=the velocity of light in the medium.
Terrestrial lightning generates very-low-frequency radio waves ranging in frequency from 1 kHz to 30 kHz known as whistlers from bouncing off the ionosphere, and wider-band emissions known as sferics. Much of this would exist in the very low frequency category of radio waves, for which literature values of refractive index is harder to determine. Using the formula given in this paper, the refractive index for radio waves in similar conditions is 1.000315, which equates to a speed of light of 299698.0 km/s (or 186223.7 miles/s). This means that to get the distance in kilometers, the time difference between flash and radio burst should instead be multiplied by 13.6 billion (or 8.45 billion for miles).
Using a setup similar to that used for passive radar, it would theoretically be possible to use this effect to determine the distance to a source of extremely short bursts of visible light and radio waves, although one might have to compensate for the tiny effect time with tricks involving phase detection or receiver harmonics. Large inaccuracies may propagate from the inconsistency of air pressure, temperature, electron density, humidity in the atmosphere, even local temperature of the receiver, which may need to be taken into account.
The joke is that it is impractical for people who haven't spent time with radio engineering, because they haven't heard of measuring such small time intervals (on the scale of 0.1 nanoseconds per kilometer or mile) and because they don't know how to detect radiation outside the visible spectrum, which can be done with a $20 radio dongle. An upconverter may be needed to measure the low-frequency details, and possibly building one's own loop antenna to pick them up in the first place. It would be difficult to use such a "rule of thumb" for somebody not already exposed to either the amateur software-defined-radio scene or professional hardware.
Although lightning lasts about 60 to 70 microseconds, during which time the signals we receive would rise and fall somewhat erratically, a software-defined radio can sample the phase and strength of the signal in detail during this time and provide a record of it for comparison with a recording at a different frequency. A more expensive radio would make life easier, as a sampling rate of at least a few GHz would allow for the time discrepancy to be measured directly using the onset of the signal, rather than possibly inferred from phase differences at different frequencies.
For the purpose of the joke, the "5 billion" value used in the comic is a fair estimate which also references the original rule of 5 seconds per mile nicely, though the result can have a huge margin of error depending on actual conditions (temperature, humidity, etc.), as the title text suggests ("the index of radio refraction does have a lot of variation").
The title text suggests another method of calculating the distance to lightning. Since the absorption of light is also different in different wavelengths, it would be possible to calculate the difference by comparing the brightness instead of relative delay. This would, however, require the knowledge of the emission spectrum of lightning and attenuation ratios of different wavelengths (which would both vary across conditions).
Transcript[edit]
- [Cueball and Megan stand on either side of a window, observing a bolt of lightning in a dark sky.]
- Cueball: What's that trick for telling how many miles away lightning is?
- Megan: Just count the seconds between the visible flash and the radio wave burst, then multiply by 5 billion.
Discussion
Calculations I used:
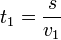
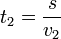
Substract:
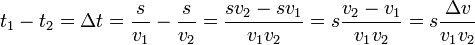
Therefore
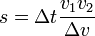
I evaluated  and it came to be 13.6 billion. Can someone verify it's correct? 172.68.51.112 13:08, 1 August 2018 (UTC)
and it came to be 13.6 billion. Can someone verify it's correct? 172.68.51.112 13:08, 1 August 2018 (UTC)
- The comic begins with the question "how many miles away", so converting to kilometers isn't the right calculation.172.69.71.24 17:06, 1 August 2018 (UTC)
I used refractive index for visible light of 1.000277 (air at STP as opposed to 0C 1atm) and arrived at around 7.9 billion instead. Refractive index of 1.000337 is then required for the radio waves for the comic to be correct. 172.68.11.221 13:46, 1 August 2018 (UTC)
- Do you mean 7.9 billion to convert to miles or to kilometers? Because my 13.6 bilion is to kilometers.
- I'm sure the actual comic is referring to miles and 5 billion was picked to match with the "divide by five" rule for miles. 172.69.70.131 13:59, 1 August 2018 (UTC)
- I did mean kilometers. If we use miles, 1.000314 fits almost precisely! (5.04 billion) 172.68.11.17 14:42, 1 August 2018 (UTC)
If you can count several seconds, as is suggested in the comic, the flash is still billions of miles away, the widest possible distance between Earth and Neptune is about 5 billion km. Sebastian --172.68.110.40 14:51, 1 August 2018 (UTC)
- Not to mention that there's not a lot of air within a few billion miles of earth, so the dispersion will be much lower for all but the last 100-ish miles, AFAIK.172.68.54.142 20:12, 1 August 2018 (UTC)
- Also, while Jupiter has VERY gigantic storms, they are still too small to see the lightning from them from Earth. -- Hkmaly (talk) 23:17, 1 August 2018 (UTC)
Do you really need to know the spectrum of the flash? If we assume that a flash contains UV and X-ray radiation and that the visible light is generated at the same time as the UV or X-ray radiation then you only need to know the refractive index of light/UV/X-ray in air under the same temperature conditions and not the exact spectrum. Condor70 (talk)
- I initially made the mistake of thinking this referred to time difference between visible and UV/X-ray, but it specifically says "brightness." If you want to compare the brightness at a distance to the brightness at the source you'll need to know the brightness at the source, i.e. the spectrum of the flash itself. With this technique you don't need to know the dispersion "only" the relative attenuation, but I suspect that would be a more error-prone measurement.172.68.54.142 18:54, 1 August 2018 (UTC)
I understand the joke Randall was going for, but have a problem with the wording. "Count the number of seconds" won't work for fractions of anything. "Measure" would work, but spoils the gag a bit. Counting numbers are integers; counting the seconds between the visible and radio frequency flashes will give you zero. 172.69.71.24 17:00, 1 August 2018 (UTC)
- You're certainly correct, but the joke works (for me at least) by its comparison to the standard rule of counting seconds, and humans are not generally precise enough to resolve better than one second. By keeping Megan's wording as close to the customary rule as possible I think it optimizes the humor. That "Billion" at the end is the whole joke for me, the replacement of "sound" with "radio wave" can be glossed-over on first reading, until you get to the unexpected extra 9 orders of magnitude in the conversion.172.68.54.142 18:54, 1 August 2018 (UTC)
- No, they would've been correct if she'd said "count the number of seconds" but she said "count the seconds".It's part of the joke, because it's correct, just completely impractical, because you'd be "counting" something like 10^(-10) seconds--172.68.132.47 07:23, 5 August 2018 (UTC)
- Just realized I also glossed-over the replacement of "divide" with "multiply." The brain is a funny thing.172.68.54.142 20:07, 1 August 2018 (UTC)
- I took the "count the number of seconds" to be part of the joke, or rather Randall setting us up for the joke. Redbelly98 (talk) 02:18, 6 August 2018 (UTC)
Do these account for the air pressure variability common in most thunderstorms?
I think explanation and transcript are pretty complete now. 172.68.51.112 20:58, 1 August 2018 (UTC)
- There is the additional problem that a flash is no instantaneous, but progresses at a fraction of the speed of light. Who says that radio waves and light at different wavelenghts or xrays have their maximum at the same moment? ;-) --162.158.91.59 08:05, 2 August 2018 (UTC)
Here's a variation of the calculation above that simplifies numeric evaluation:
The refractive index is defined as  , so
, so 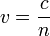 and thus
and thus 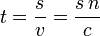 .
.

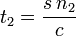
Subtract:
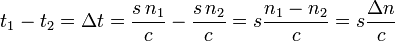
Therefore

and the factor we want to calculate is
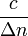
With the numbers given in the sources in the main text:
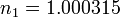
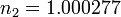

For kilometers: 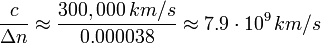
For miles: 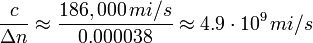
Chrisahn (talk) 18:28, 2 August 2018 (UTC)
- Nice one. I didn't think to use the refractive indicies directly. 172.68.51.118 22:22, 2 August 2018 (UTC)
- Agreed, nice clear analysis by Chrisahn. I'd like to suggest a couple of corrections regarding the index values:
- n for air at 0 C, 1 atm, is closer to 1.000292, according to both the Wikipedia link and also the "Simple Shop-floor Formula" given by NIST at the bottom of this site. This would give a
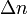 of 0.000023, and a time-to-distance conversion value of
of 0.000023, and a time-to-distance conversion value of  mi/s.
mi/s. - Thunderstorms rarely occur at 0 C. Using values for 30 C (86 F) instead, we have 1.000261 for air (from the simple NIST formula) and 1.000429 for radio waves (from Table 1, p. 8 of the Rueger paper). This gives a
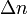 of 0.000168, and a time-to-distance conversion value of
of 0.000168, and a time-to-distance conversion value of  mi/s.
mi/s.
- n for air at 0 C, 1 atm, is closer to 1.000292, according to both the Wikipedia link and also the "Simple Shop-floor Formula" given by NIST at the bottom of this site. This would give a
- This suggests that the conversion value is the desired 5 billion for some temperature between 0 and 30 C. Linear interpolation of the above suggests this temperature is about 13 C or 55 F [EDIT: See note after this comment]. More to the point, the conversion value varies too strongly with temperature for there to be a simple rule. That being said, I do like that the 5 billion figure ties in nicely with the familiar (in USA) divide by 5 rule. Redbelly98 (talk) 02:18, 6 August 2018 (UTC)
- NOTE: Please ignore the linearly interpolated "13 C" above. It turns out n for radio waves is a highly nonlinear function of temperature. Plus the 1/Δn dependence -- where Δn changes by a factor of 7 or 8 -- makes the nonlinearity even worse. --Redbelly98 (talk) 01:05, 7 August 2018 (UTC)
Assumptions on the medium properties sound?
Refractive index of *dry* air might be pretty close to 1 for both light and RF EM waves, but:
Let's assume that the air is humid, if not even full of water drops. After all, lightning.
Let's further assume that an air/water mixture or solution has electromagnetic properties between these two materials.
In water, refractive index for light is about 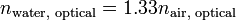 , (as easily demonstrated by the optical refractive effects); for RF, we typically use values of
, (as easily demonstrated by the optical refractive effects); for RF, we typically use values of 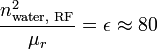 . So,
. So, 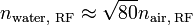 .
.
Let's assume a 10⁻³ "EM-effective" water content in the comic air.
That would lead to 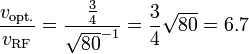 .
.
- While the humidity (amount of water vapor) is certainly higher during the rain, I don't think that would count as a proper "water-air mixture". Wikipedia says that "Violent rain" is above 5 cm/h. If you divide it by 3600 (to get cm/s), and then imagine stretching that all the way to the cloud, you'll find out there's not that much water at given moment in the air. 172.68.51.112 19:12, 1 August 2018 (UTC)
- Great point. To finish the calculation let's use a typical terminal velocity for a large raindrop (it's a big storm, I'm sure) of 9m/s. 0.05 m/hr / 3600 s/hr / 9 m/s = 0.00015% water by volume. Sure seems like more than that when I have to drive through it! Then it seems more like [1].172.68.54.142 20:32, 1 August 2018 (UTC)
we can't detect radiation outside the visible spectrum without very specialized instruments Something that I think was overlooked in the explanation is that while humans can't *directly* sense radio waves, there are devices called "radios" which at one point in time were fairly commonly owned by humans, whose whole purpose is to detect encoded radio waves and convert them into sounds which humans can sense. I.e. you hear static during an electrical storm. So you could listen for the static and compare that to the flash... if you were fast enough. 172.68.54.64 14:22, 3 August 2018 (UTC) (newbie)
- But radios ARE specialized equipment. 172.68.51.52 10:35, 4 August 2018 (UTC)
- Ehh... I see your point, but I'm not sure I'm *really* convinced. In my mind, a Gamma Ray Spectrometer is specialized equipment. People don't normally have them in their house or car. Radios are (or, at least, *were*) very common. But you're right, it says specialized instrument, not "rare" instrument. I'm not changing the explanation, just wanted to point out for those geeky enough to read the comments that for normal people, *detecting* the radio wave output lightning is doable without buying extra equipment one doesn't normally have in the home. Detecting the difference between the flash and the static on the radio is where it gets impractical. 172.68.54.64 15:01, 6 August 2018 (UTC) (newbie)
- Keep in mind, if you're using radios (normal consumer receiver/amp/speaker setups) to pick up the radio-frequency emissions, and eyes the visible light, you have to add the speed of sound back into the equation, based on the distance between the speaker and your ear. Plus, there would inevitably be the delay for the circuitry in the radio, plus the delay in your perceptions. At the nanosecond scale, the difference in length between optic and auditory tracts in your cerebral innervation and brain would be more than enough to swamp any effect of the lightspeed variation. Thus: specialized equipment would be needed. Nitpicking (talk) 20:02, 25 July 2022 (UTC)
- Unless you're listening to digital radio (with decoding delays, which is why you shouldn't depend upon DAB audio of "The Pips", but probably also won't reliably render the interference derived from the lightning) the circuitry in the radio won't significantly delay things. It's barely buffered by FM or AM being processed to extract the raw audio (original, or pseudo-original interpretation of the intergerence) and the wiring between components barely adds anything. 570 nanoseconds per 100m of wire (for a 1Mhz signal, lower frequencies can take longer, but not that much), is one estimate of wire-lenth delay, and you probably don't have that much length wrapped around inside your transistor radio. (Elsewhere, 75% of c is quoted, in saying that it's maybe a couple of tens of milliseconds delay across a distance between New York and Los Angeles, by a probably non-direct cable, after removing relay and protocol-processing delays.)
- Obviously when multiplying by 5 (or more) billion, the increased (or decreased) delay does become significantly more maladjusted (and significant) from the original premise, but that surely applies far more to the audio/perceptive/reactive delays, however you calculate those. 172.70.85.13 23:37, 25 July 2022 (UTC)
Whoops!
I always thought it was 1 second per mile. I didn't know about the 'divide by 5" part. These Are Not The Comments You Are Looking For (talk) 01:23, 5 August 2018 (UTC)
- Storms just became 5 times more scary for you :) 188.114.103.95 12:12, 6 August 2018 (UTC)
Actually...[edit]
There's a citizen science project called blitzortung.org that uses special radio receivers to sample the lightning 's signature, compare it with the other receivers and use gps time to triangulate its position! --141.101.69.175 12:37, 18 July 2021 (UTC)

