Difference between revisions of "2059: Modified Bayes' Theorem"
m (→Transcript) |
(→Explanation: Add why equation makes no sense as is and a rewrite that makes more sense.) |
||
| Line 26: | Line 26: | ||
<math>1-P(C)</math> is the probability that you are using the theorem incorrectly. | <math>1-P(C)</math> is the probability that you are using the theorem incorrectly. | ||
| + | |||
| + | As an equation, the rewritten form makes no sense. <math>P(H \mid X) = P(H)(1-P(C)) + P(H \mid X)P(C)</math> is strangely self-referential and reduces to the piecewise equation <math>\begin{cases}P(H \mid X) = P(H) & P(C) \neq 1 \\ 0 = 0 & P(C) = 1 \end{cases}</math>. However, the Modified Bayes Theorem includes an extra variable not listed in the conditioning, so a person with an AI background might understand that Randal was trying to write an expression for updating <math>P(H \mid X)</math> with knowledge of <math>C</math> i.e. <math>P(H \mid X,C)</math>, the belief in the hypothesis given the observation <math>X</math> and the confidence that you were applying Bayes' theorem correctly <math>C</math>, for which the expression <math>P(H \mid X,C) = P(H)(1-P(C)) + P(H \mid X)P(C)</math> makes some intuitive sense. | ||
The title text suggests that an additional term should be added for the probability that the Modified Bayes Theorem is correct. But that's *this* equation, so it would make the formula self-referential. It could also result in an infinite regress -- we'd need another term for the probability that the version with the probability added is correct, and another term for that version, and so on. It's also unclear what the point of using an equation we're not sure of is (although sometimes we can: {{w|Newton's Laws}} are not as correct as the Einstein's {{w|Theory of Relativity}} but they're a reasonable approximation in most circumstances}. | The title text suggests that an additional term should be added for the probability that the Modified Bayes Theorem is correct. But that's *this* equation, so it would make the formula self-referential. It could also result in an infinite regress -- we'd need another term for the probability that the version with the probability added is correct, and another term for that version, and so on. It's also unclear what the point of using an equation we're not sure of is (although sometimes we can: {{w|Newton's Laws}} are not as correct as the Einstein's {{w|Theory of Relativity}} but they're a reasonable approximation in most circumstances}. | ||
Revision as of 18:57, 15 October 2018
| Modified Bayes' Theorem |
 Title text: Don't forget to add another term for "probability that the Modified Bayes' Theorem is correct." |
Explanation
| |
This explanation may be incomplete or incorrect: Please edit the explanation below and only mention here why it isn't complete. Do NOT delete this tag too soon. If you can address this issue, please edit the page! Thanks. |
Bayes' theorem is:
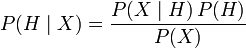 ,
where
,
where
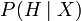 is the belief that
is the belief that 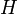 is true given that
is true given that 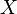 is true. The posterior probability of
is true. The posterior probability of 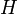 .
.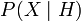 is the belief that
is the belief that 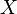 is true given that
is true given that 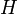 is true.
is true.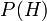 and
and 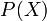 are the beliefs that
are the beliefs that 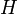 and
and 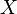 respectively are true independent of other evidence. They are the prior probability of H and X respectively.
respectively are true independent of other evidence. They are the prior probability of H and X respectively.
If 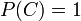 the modified theorem reverts to the original Bayes' theorem (which makes sense, as a probability one would mean certainty that you are using Bayes' theorem correctly).
the modified theorem reverts to the original Bayes' theorem (which makes sense, as a probability one would mean certainty that you are using Bayes' theorem correctly).
If 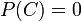 the modified theorem becomes
the modified theorem becomes  , which says that the belief in your hypothesis is not affected by the result of the observation (which makes sense because you're certain you're misapplying the theorem so the outcome of the calculation shouldn't affect your belief.)
, which says that the belief in your hypothesis is not affected by the result of the observation (which makes sense because you're certain you're misapplying the theorem so the outcome of the calculation shouldn't affect your belief.)
This happens because, if you apply the original theorem, the modified theorem can be rewritten as: 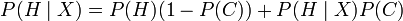 . This is the linear-interpolated weighted average of the belief you had before the calculation and the belief you would have if you applied the theorem correctly. This goes smoothly from the not believing your calculation at all, keeping the same belief as before if
. This is the linear-interpolated weighted average of the belief you had before the calculation and the belief you would have if you applied the theorem correctly. This goes smoothly from the not believing your calculation at all, keeping the same belief as before if 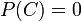 to changing your belief exactly as Bayes' theorem suggests when
to changing your belief exactly as Bayes' theorem suggests when 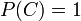 .
.
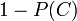 is the probability that you are using the theorem incorrectly.
is the probability that you are using the theorem incorrectly.
As an equation, the rewritten form makes no sense. 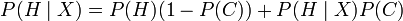 is strangely self-referential and reduces to the piecewise equation
is strangely self-referential and reduces to the piecewise equation 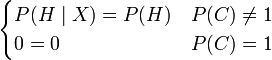 . However, the Modified Bayes Theorem includes an extra variable not listed in the conditioning, so a person with an AI background might understand that Randal was trying to write an expression for updating
. However, the Modified Bayes Theorem includes an extra variable not listed in the conditioning, so a person with an AI background might understand that Randal was trying to write an expression for updating 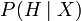 with knowledge of
with knowledge of  i.e.
i.e.  , the belief in the hypothesis given the observation
, the belief in the hypothesis given the observation 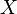 and the confidence that you were applying Bayes' theorem correctly
and the confidence that you were applying Bayes' theorem correctly  , for which the expression
, for which the expression  makes some intuitive sense.
makes some intuitive sense.
The title text suggests that an additional term should be added for the probability that the Modified Bayes Theorem is correct. But that's *this* equation, so it would make the formula self-referential. It could also result in an infinite regress -- we'd need another term for the probability that the version with the probability added is correct, and another term for that version, and so on. It's also unclear what the point of using an equation we're not sure of is (although sometimes we can: Newton's Laws are not as correct as the Einstein's Theory of Relativity but they're a reasonable approximation in most circumstances}.
Transcript
| |
This transcript is incomplete. Please help editing it! Thanks. |
- Modified Bayes' theorem:
- P(H|X) = P(H) × (1 + P(C) × ( P(X|H)/P(X) - 1 ))
- H: Hypothesis
- X: Observation
- P(H): Prior probability that H is true
- P(X): Prior probability of observing X
- P(C): Probability that you're using Bayesian statistics correctly
Discussion
Right now the layout is awful:
- "If
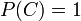 the..."
the..." - should look like this:
- "If P(C)=1 the..."
But there is more wrong right now. Look at a typical Wikipedia article, the Math-extension should be used for formulas but not in the floating text. --Dgbrt (talk) 20:03, 15 October 2018 (UTC)
- Credit for a good explanation though. It made perfect sense to me, even though I didn't understand it. 162.158.167.42 04:14, 16 October 2018 (UTC)
I removed this, because it makes no sense:
- As an equation, the rewritten form makes no sense.
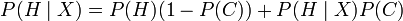 is strangely self-referential and reduces to the piecewise equation
is strangely self-referential and reduces to the piecewise equation 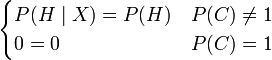 . However, the Modified Bayes Theorem includes an extra variable not listed in the conditioning, so a person with an AI background might understand that Randal was trying to write an expression for updating
. However, the Modified Bayes Theorem includes an extra variable not listed in the conditioning, so a person with an AI background might understand that Randal was trying to write an expression for updating  with knowledge of
with knowledge of  i.e.
i.e.  , the belief in the hypothesis given the observation
, the belief in the hypothesis given the observation  and the confidence that you were applying Bayes' theorem correctly
and the confidence that you were applying Bayes' theorem correctly  , for which the expression
, for which the expression  makes some intuitive sense.
makes some intuitive sense.
Between removing it and posting here, I think that I've figured out what it's saying. But it comes down to criticizing a mistake made in an earlier edit by the same editor, so I'll just fix that mistake instead.
—TobyBartels (talk) 13:03, 16 October 2018 (UTC)
What about examples of correct and incorrect use of Bayes' Theorem? I don't feel equal to executing that, but DNA evidence in a criminal case could be illuminating. As a sketch, it may show that of 7 billion people alive today, the blood at the scene came from any one of just 10,000 people of which the accused is one. Interesting, but not absolute. At least 9,999 of the 10,000 are innocent. Probability of mistake or malfeasance by the testing laboratory also needs to be considered. Then there's sports drug testing, disease screening with imperfect tests and rare true positives, etc. [email protected] 141.101.76.82 09:42, 17 October 2018 (UTC)
Where is the next comic button for this page? IYN (talk) 15:46, 17 October 2018 (UTC)
