271: Powers of One
| Powers of One |
 Title text: It's kinda Zen when you think about it, if you don't think too hard. |
Explanation
This is a parody of the short documentary "Powers of 10": the original one can be found at http://www.powersof10.com/film.
Like in the documentary, the comic features a man and a woman on a blanket, during a picnic. Then, the zoom level of the image should change... but, while in the documentary it changes by 10 times at every frame (hence the name "Powers of 10": 1x, 10x, 100x ...), in the comic powers of 1 are used: since every power of 1 is always 1, the image doesn't change at all.
So, a series of identical images is shown.
The title text says that while this idea may seem profound (or "Zen", which is commonly used in American slang to mean "profound") but quickly loses any pretensions to actually being profound when you take a second look.
Transcript
- [A sequence, presumably continuing endlessly in both directions, of identical images of a couple lying on a chequered blanket, with a picnic basket, on grass. Each image has a rule at the bottom giving measurements in meters, with the scale in terms of 1 to a particular power. The powers visible are the -1th (part), 0th-2nd, and 3rd (part).]
Discussion
I got the math joke but did not know about the documentary, very interesting. 184.66.160.91 04:26, 27 August 2013 (UTC)
I want a "Powers of 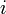 " documentary. 172.68.132.95 08:21, 27 February 2019 (UTC)
" documentary. 172.68.132.95 08:21, 27 February 2019 (UTC)
- Basiclly it will in each iteration rotate image 90 degrees. /*
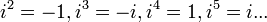
- Ans so on */ 172.69.55.52 09:28, 4 July 2019 (UTC)
- What about a "Powers of 2i" documentary? ColorfulGalaxy (talk) 08:59, 13 December 2022 (UTC)
- This is basically a "Powers of ((i)^2)^2" documentary. B for brain (talk) (youtube channel wobsite (supposed to be a blag) 18:28, 21 April 2024 (UTC)
Is it a coincidence, that this is selected for comic 271, while 2, 7 and 1 are the first digits of "e", which is also a very common base in Exponentiation? --Lupo (talk) 14:02, 11 December 2019 (UTC)
I once remember seeing someone wrongly saying "one to the fourth power" instead of "ten to the fourth power",[citation needed] probably on a show or a movie. I don't remember the name of the show. Edit: It may be cited on Numberphile. --ColorfulGalaxy (talk) 08:59, 13 December 2022 (UTC)
