Talk:2027: Lightning Distance
Calculations I used:
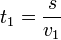
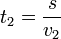
Substract:
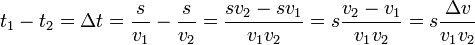
Therefore
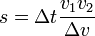
I evaluated  and it came to be 13.6 billion. Can someone verify it's correct? 172.68.51.112 13:08, 1 August 2018 (UTC)
and it came to be 13.6 billion. Can someone verify it's correct? 172.68.51.112 13:08, 1 August 2018 (UTC)
- The comic begins with the question "how many miles away", so converting to kilometers isn't the right calculation.172.69.71.24 17:06, 1 August 2018 (UTC)
I used refractive index for visible light of 1.000277 (air at STP as opposed to 0C 1atm) and arrived at around 7.9 billion instead. Refractive index of 1.000337 is then required for the radio waves for the comic to be correct. 172.68.11.221 13:46, 1 August 2018 (UTC)
- Do you mean 7.9 billion to convert to miles or to kilometers? Because my 13.6 bilion is to kilometers.
- I'm sure the actual comic is referring to miles and 5 billion was picked to match with the "divide by five" rule for miles. 172.69.70.131 13:59, 1 August 2018 (UTC)
- I did mean kilometers. If we use miles, 1.000314 fits almost precisely! (5.04 billion) 172.68.11.17 14:42, 1 August 2018 (UTC)
If you can count several seconds, as is suggested in the comic, the flash is still billions of miles away, the widest possible distance between Earth and Neptune is about 5 billion km. Sebastian --172.68.110.40 14:51, 1 August 2018 (UTC)
- Not to mention that there's not a lot of air within a few billion miles of earth, so the dispersion will be much lower for all but the last 100-ish miles, AFAIK.172.68.54.142 20:12, 1 August 2018 (UTC)
- Also, while Jupiter has VERY gigantic storms, they are still too small to see the lightning from them from Earth. -- Hkmaly (talk) 23:17, 1 August 2018 (UTC)
Do you really need to know the spectrum of the flash? If we assume that a flash contains UV and X-ray radiation and that the visible light is generated at the same time as the UV or X-ray radiation then you only need to know the refractive index of light/UV/X-ray in air under the same temperature conditions and not the exact spectrum. Condor70 (talk)
- I initially made the mistake of thinking this referred to time difference between visible and UV/X-ray, but it specifically says "brightness." If you want to compare the brightness at a distance to the brightness at the source you'll need to know the brightness at the source, i.e. the spectrum of the flash itself. With this technique you don't need to know the dispersion "only" the relative attenuation, but I suspect that would be a more error-prone measurement.172.68.54.142 18:54, 1 August 2018 (UTC)
I understand the joke Randall was going for, but have a problem with the wording. "Count the number of seconds" won't work for fractions of anything. "Measure" would work, but spoils the gag a bit. Counting numbers are integers; counting the seconds between the visible and radio frequency flashes will give you zero. 172.69.71.24 17:00, 1 August 2018 (UTC)
- You're certainly correct, but the joke works (for me at least) by its comparison to the standard rule of counting seconds, and humans are not generally precise enough to resolve better than one second. By keeping Megan's wording as close to the customary rule as possible I think it optimizes the humor. That "Billion" at the end is the whole joke for me, the replacement of "sound" with "radio wave" can be glossed-over on first reading, until you get to the unexpected extra 9 orders of magnitude in the conversion.172.68.54.142 18:54, 1 August 2018 (UTC)
- Just realized I also glossed-over the replacement of "divide" with "multiply." The brain is a funny thing.172.68.54.142 20:07, 1 August 2018 (UTC)
Do these account for the air pressure variability common in most thunderstorms?
I think explanation and transcript are pretty complete now. 172.68.51.112 20:58, 1 August 2018 (UTC)
- There is the additional problem that a flash is no instantaneous, but progresses at a fraction of the speed of light. Who says that radio waves and light at different wavelenghts or xrays have their maximum at the same moment? ;-) --162.158.91.59 08:05, 2 August 2018 (UTC)
Assumptions on the medium properties sound?
Refractive index of *dry* air might be pretty close to 1 for both light and RF EM waves, but:
Let's assume that the air is humid, if not even full of water drops. After all, lightning.
Let's further assume that an air/water mixture or solution has electromagnetic properties between these two materials.
In water, refractive index for light is about 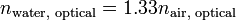 , (as easily demonstrated by the optical refractive effects); for RF, we typically use values of
, (as easily demonstrated by the optical refractive effects); for RF, we typically use values of 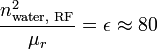 . So,
. So, 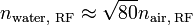 .
.
Let's assume a 10⁻³ "EM-effective" water content in the comic air.
That would lead to 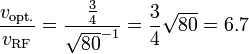 .
.
- While the humidity (amount of water vapor) is certainly higher during the rain, I don't think that would count as a proper "water-air mixture". Wikipedia says that "Violent rain" is above 5 cm/h. If you divide it by 3600 (to get cm/s), and then imagine stretching that all the way to the cloud, you'll find out there's not that much water at given moment in the air. 172.68.51.112 19:12, 1 August 2018 (UTC)
- Great point. To finish the calculation let's use a typical terminal velocity for a large raindrop (it's a big storm, I'm sure) of 9m/s. 0.05 m/hr / 3600 s/hr / 9 m/s = 0.00015% water by volume. Sure seems like more than that when I have to drive through it! Then it seems more like [1].172.68.54.142 20:32, 1 August 2018 (UTC)
