Difference between revisions of "2974: Storage Tanks"
(→Explanation) |
|||
| (17 intermediate revisions by 12 users not shown) | |||
| Line 10: | Line 10: | ||
==Explanation== | ==Explanation== | ||
| − | {{ | + | {{w|Calculus}} is a branch of mathematics which deals with continuously changing values. In order to demonstrate the application of this sort of math, introductory courses will commonly use physical examples to show how equations can be applied in real life. A [https://www.haywardflowcontrol.com/media/contentmanager/content//downloads//VessTime.pdf common example of such a problem] is to postulate a tank full of liquid, with a hole near the bottom, and ask the students to calculate how long it will take the tank to empty (generally assuming a cylindrical tank with the top at atmospheric pressure, leaking a low-viscosity fluid like water at a normal temperature flowing through a round hole.) The important variables are threefold: the radius of the tank, the height of the fluid above the hole, and the size of the hole. |
| − | |||
| − | + | In this case, the change in the liquid level is a function of the rate of flow through the hole, which is a function of the fluid pressure at the entrance to the hole (in accordance with {{w|Torricelli's law}}), and that pressure is a function of the remaining level of liquid. Accordingly, the amount of fluid left in the tank above the hole will follow a quadratic decay, a concept covered in calculus courses. A student with a mastery of foundational principles of calculus should be able to calculate the decline in tank level. More advanced versions of the problem might involve (A) one tank draining into a second, which drains to the ground, or (B) a sealed tank, in which air pressure at the top falls as the tank drains. | |
| − | + | As mentioned, many STEM teachers like to use real-world examples, ideally physical demonstrations, to make abstract concepts more memorable for their students. A teacher might fill a jug with water, open a hole in the side, and invite students to compare the observed rate of draining to their calculations. This comic suggests that [[Miss Lenhart]] has taken this idea to extremes, having entered an industrial site and drilled a hole into a large, liquid-filled vat. One assumes that her class is either watching from afar, or that the leak is being somehow filmed. | |
| − | + | The conversation between the employees in hardhats implies that there's a rash of calculus teachers conducting similar demonstrations, to the point that the primary job of the head of security is to prevent this pedagogically-motivated destruction. In real life, this vandalism would be serious, with safety risks from damaged vats, pressurized liquid, or hazardous contents (note the hazard warning (⚠) on the tank). | |
| − | The title text jokingly alludes to the fact that by maintaining a constant pressure | + | The title text jokingly alludes to the fact that by maintaining a constant pressure at the level of the leak, the rate of flow would also become constant, and the decline in level would therefore become linear, greatly simplifying the problem and eliminating the need for calculus. This easier version of the problem would presumably deter calculus teachers from using it as a demonstration — though it might attract similarly adventurous algebra teachers. |
| − | |||
| − | |||
===Analysis and Calculation=== | ===Analysis and Calculation=== | ||
| Line 27: | Line 24: | ||
* Tank height above hole: ~20 feet | * Tank height above hole: ~20 feet | ||
* Tank radius: ~6 feet | * Tank radius: ~6 feet | ||
| − | * Type of drill bit: Normal (not a hole saw) | + | * Type of drill bit: Normal twist drill bit (not a hole saw) |
* Size of drill bit: 1 inch (largest commonly available twist drill bit) | * Size of drill bit: 1 inch (largest commonly available twist drill bit) | ||
* Goal of Miss Lenhart: To demonstrate quadratic decay to her students | * Goal of Miss Lenhart: To demonstrate quadratic decay to her students | ||
| − | With a tank that is 20 feet high, has a 6-foot radius, and a 1-inch diameter drill hole, it would take approximately 21.5 hours for the tank to empty completely — too long for a suitable class demonstration | + | With a tank that is 20 feet high, has a 6-foot radius, and a 1-inch diameter drill hole, it would take approximately 21.5 hours for the tank to empty completely — too long for a suitable class demonstration — though maybe filmed as a time-lapse video? — and nonetheless likely to be fixed by nearby workers who notice the leak. |
| + | |||
| + | To drain the tank in 36 minutes would take a 6-inch diameter hole. | ||
| + | |||
| + | Thus there's an apparent mismatch between the drill bit size, gushing liquid stream, and practicality of this real-world demonstration. The viscosity & density of the liquid is also an unknown factor; for ease of calculation, calculus problems tend to assume that the liquid is either ordinary water (which, by definition, has a density of 1.00* (1 kg/liter (8.35 lbs/gallon)) and a viscosity of 1.001 millipascal seconds) or a mixture mostly composed of water (depending on what exactly else it contains, such as dissolved solids or just other | ||
| − | + | * at 20°C (68°F) & sea-level air pressure | |
| − | + | One explanation is that she was able to drill a couple dozen approx. 1-inch holes in a short time, while toxic liquid is gushing out, but the drill doesn't appear to be dripping wet. | |
| − | + | But the most likely explanation to all this is that Randall didn't think through the drill and drill bit size in relation to the apparent hole size, leaving it only to nitpicky editors of a comic explainer website to even notice and care. | |
| − | + | Or, the tank simply is not full at the moment the teacher drills the hole. | |
==Transcript== | ==Transcript== | ||
Latest revision as of 09:58, 29 September 2024
| Storage Tanks |
 Title text: We're considering installing a pressurization system to keep the tanks at constant pressure solely to deter them. |
Explanation[edit]
Calculus is a branch of mathematics which deals with continuously changing values. In order to demonstrate the application of this sort of math, introductory courses will commonly use physical examples to show how equations can be applied in real life. A common example of such a problem is to postulate a tank full of liquid, with a hole near the bottom, and ask the students to calculate how long it will take the tank to empty (generally assuming a cylindrical tank with the top at atmospheric pressure, leaking a low-viscosity fluid like water at a normal temperature flowing through a round hole.) The important variables are threefold: the radius of the tank, the height of the fluid above the hole, and the size of the hole.
In this case, the change in the liquid level is a function of the rate of flow through the hole, which is a function of the fluid pressure at the entrance to the hole (in accordance with Torricelli's law), and that pressure is a function of the remaining level of liquid. Accordingly, the amount of fluid left in the tank above the hole will follow a quadratic decay, a concept covered in calculus courses. A student with a mastery of foundational principles of calculus should be able to calculate the decline in tank level. More advanced versions of the problem might involve (A) one tank draining into a second, which drains to the ground, or (B) a sealed tank, in which air pressure at the top falls as the tank drains.
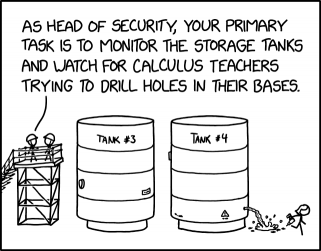
As mentioned, many STEM teachers like to use real-world examples, ideally physical demonstrations, to make abstract concepts more memorable for their students. A teacher might fill a jug with water, open a hole in the side, and invite students to compare the observed rate of draining to their calculations. This comic suggests that Miss Lenhart has taken this idea to extremes, having entered an industrial site and drilled a hole into a large, liquid-filled vat. One assumes that her class is either watching from afar, or that the leak is being somehow filmed.
The conversation between the employees in hardhats implies that there's a rash of calculus teachers conducting similar demonstrations, to the point that the primary job of the head of security is to prevent this pedagogically-motivated destruction. In real life, this vandalism would be serious, with safety risks from damaged vats, pressurized liquid, or hazardous contents (note the hazard warning (⚠) on the tank).
The title text jokingly alludes to the fact that by maintaining a constant pressure at the level of the leak, the rate of flow would also become constant, and the decline in level would therefore become linear, greatly simplifying the problem and eliminating the need for calculus. This easier version of the problem would presumably deter calculus teachers from using it as a demonstration — though it might attract similarly adventurous algebra teachers.
Analysis and Calculation[edit]
Observation of the comic suggests the following assumptions:
- Tank height above hole: ~20 feet
- Tank radius: ~6 feet
- Type of drill bit: Normal twist drill bit (not a hole saw)
- Size of drill bit: 1 inch (largest commonly available twist drill bit)
- Goal of Miss Lenhart: To demonstrate quadratic decay to her students
With a tank that is 20 feet high, has a 6-foot radius, and a 1-inch diameter drill hole, it would take approximately 21.5 hours for the tank to empty completely — too long for a suitable class demonstration — though maybe filmed as a time-lapse video? — and nonetheless likely to be fixed by nearby workers who notice the leak.
To drain the tank in 36 minutes would take a 6-inch diameter hole.
Thus there's an apparent mismatch between the drill bit size, gushing liquid stream, and practicality of this real-world demonstration. The viscosity & density of the liquid is also an unknown factor; for ease of calculation, calculus problems tend to assume that the liquid is either ordinary water (which, by definition, has a density of 1.00* (1 kg/liter (8.35 lbs/gallon)) and a viscosity of 1.001 millipascal seconds) or a mixture mostly composed of water (depending on what exactly else it contains, such as dissolved solids or just other
* at 20°C (68°F) & sea-level air pressure
One explanation is that she was able to drill a couple dozen approx. 1-inch holes in a short time, while toxic liquid is gushing out, but the drill doesn't appear to be dripping wet.
But the most likely explanation to all this is that Randall didn't think through the drill and drill bit size in relation to the apparent hole size, leaving it only to nitpicky editors of a comic explainer website to even notice and care.
Or, the tank simply is not full at the moment the teacher drills the hole.
Transcript[edit]
- [Two guards with helmets are standing on scaffolding to the left of two large tanks with labels at the top. The tanks are cylindrical with a smaller base than the tank above it. The left tank has a small sign with unreadable text and near the bottom of the right tank there is a triangular warning sign with an exclamation mark inside it and a line of unreadable text below it. The guard on the left is talking to the other guard. Miss Lenhart is seen running away from the right tank with an electric drill in one hand. There is a hole in the base of the right tank which has caused the liquid inside to leak out of the tank splashing on the ground in the direction of Miss Lenhart.]
- Left guard: As head of security, your primary task is to monitor the storage tanks and watch for calculus teachers trying to drill holes in their bases.
- Label: Tank #3
- Label: Tank #4
Discussion
The symmetry of the truss intrigues me. Struts that are diagonal across the faces of the cuboids is normal, but is it a real thing to also use the body diagonal? Never seen that IRL, not sure if it makes sense from the statics. --172.70.247.82 22:16, 19 August 2024 (UTC)
- Struts as shown provide some left-right stability, but not as effectively as struts across the face would. They also provide some redundant front-back stability with the struts running along the faces. 172.68.71.90 14:47, 21 August 2024 (UTC)
- I mentally modeled the flexibility modes, and it very much depends upon whether the verticals are solid (with their resistence to bending playing a big part alongside the incident horizontals'/diagonals' exactvmethod of attachment) or are just sections of rod between a suitable receiver-'node' at each junction.
- in particular, the strength of any one of the three 'boxes' (each level between adjacent horizontal cross-sectional perimeters) is somewhat less secure, as a single level can 'fold' sideways over each side's vertical-diagonal strut (along with the respective front/back horizontals, held 'square' by the internal cross-brscing). Only the continuation and linking with the other 'boxes' really guarantees any innate stability, and if each node is free-twisting then the likely first result of any failure is that the tower topples forwards and/or backwards as it folds up due to the unbraced facing and hindside quadrilaterals.
- But it does depend a lot upon the exact nature of the linkages (which can only be guessed at), and other failure-modes could involve node-slippage if they merely grip the cross-braces to the entirely top-to-bottom poles and there's potential for sliding there instead of primarily rotation (or over-stressed failure in any given length of rod).
- The support (or additional pressure) provided by the access staircase is also probably a factor. It could even be the most important bit in holding it up! ...if firmly anchored at the other end and robust enough in itself.
- I'd definitely add other diagonals (including opposite-type body-diagonals, perhaps tied to the existing one as they pass right across each other), just to be sure. The more the better, of course, but there's probably a limit through diminishing concerns. And too many diagonals primarily in a helical pattern could concentrate forces into a particular type of rotational failure if you also add too much brace-weight in doing so. 172.70.163.120 15:07, 21 August 2024 (UTC)
Seems like a pretty menial job for the "head of security". I think he would delegate this to a security guard. Barmar (talk) 00:47, 20 August 2024 (UTC)
- They may be head of a department of one.172.70.85.139 08:50, 20 August 2024 (UTC)
The explanation mentions there might be more complex calculus examples where the shape might not be a cylinder. I think some further explanation could be added that this does not change the pressure (hydrostatic paradox) but indeed change the rate of emptying the object. If differing cross sections are relevant at all. 108.162.221.103 05:40, 20 August 2024 (UTC)
- Non-prismatic geometries are I think the ones being alluded to here, i.e a frustrum with the pointy end down will have a greater reduction in pressure for a given volume of flow towards the end than at the start, which may offset the reduction in absolute pressure. I've also seen examples where the flow rate is considered constant and the problem is to work out the fluid depth as a function of time, e.g. filling a pyramidal pool from a hose. 172.70.58.4 16:44, 20 August 2024 (UTC)
Its the most difficult job in history, even the best workers couldn't stand 1 day as head of security.I HAVE NO NAME (talk) 05:55, 20 August 2024 (UTC)
I have to admit, I thought I knew calc as I had two semesters of it, but I had to look up what he meant by this. Ouch 172.70.242.55 13:01, 20 August 2024 (UTC)student
If anyone could suggest something I can do for my class now that I can no longer drill holes in tanks, I'd appreciate the advice, thanks. Fephisto (talk) 16:18, 20 August 2024 (UTC)
Someone should do the math on the calculus problem as presented, as well as the algebra version. Laser813 (talk) 17:33, 20 August 2024 (UTC)
- Randall, like all good mathematics textbook authors, left the problem as an exercise for the reader. Does this happen often enough to warrant a tag? Paddles (talk) 05:57, 21 August 2024 (UTC)
- Yes... Transgalactic (talk) 10:10, 21 August 2024 (UTC)
Is there anyone else who thought the calculus teacher was abusing the tank as a model for the complex plane, demonstrating how to remove a singularity from a holomorphic function by puncturing the plane? I wasn't confronted with that particular tank-emptying problem in high school, so my first encounter with "holes" in maths was in complex analysis. The title text was a mystery. Transgalactic (talk) 10:10, 21 August 2024 (UTC)
As a mathematician, I'm surprised I didn't know about this idea. (It's definitely not my field!) I actually thought the flow would be constant, an algebraic problem. Oh, I'm sure I saw these types of problems in Calculus (and I remember problems like this in Differential Equations), but I thought those were just to make the math more complicated, not based in reality... So is it the weight of the liquid remaining above the hole that is the source of the pressure (i.e., would it be the same if the top of the tank were open), or is it the air pressure in the tank as the volume of liquid decreases and volume of air increases? Mathmannix (talk) 11:08, 21 August 2024 (UTC)
- A sealed-top would change the dynamics (like trying to pour the contents of a 2 litre (or whatever the US equivalent is) pop/soda bottle, it will tend to 'glug glug glug' intermittently unless you: a) incline the bottle to allow an optimum amount lf free akr back into the emltying bottle or, b) initialise the up-ended emptying with a spin sufficient to create a 'waterspout' effect up through which the replacement air can (more) freely pass.
- Though there are other possible factors, in that example, including the potential pressure of any self-releasing carbonation pressure (e.g. giving the bottle a shake, or a foreign body, before releasing the 'pour') and/or squeezing/'milking' the soft plastic container strategically to create another form of pressurised expulsion.
- For the 'classical' problem, one should probably assume sufficient inward venting (either an open/part-open top or a second hole drilled near the top to effect this purpose) as well as a reasonably unexotic liquid (neither molasses, cornstarch-mixture, anything that is actually a very fine dry powder, anything that reacts significantly with/upon air, any liquid very close to its vapour-point nor specifically supercooled helium) or any additional elements (stirrers, baffles, spongey inners, inner membranes or the contents being a layered combination of imiscable liquids of different densities that may or may not react slightly all across the interface plane). Most things that aren't actually exotic (and even a few that are, and might warrant a warning /¡\) are close enough to water to treat as if just that, at least under the further assumption that we're working at or around Standard Temperature and Pressure. But a slightly different density, viscosity and surface tension (plus the nature of the container, e.g. extreme hydrophilic or hydrophobic inner coatings where water is involved) could (in combination) drastically change the actual outcome given enough of the right kind of simultaneous differences imparted. 172.70.86.37 14:28, 21 August 2024 (UTC)
- We have these at my work: https://shop.snydernet.com/images/snyder-6370721n95402.pdf The viscosity is a huge deal, unless you can afford to waste a bunch of supply. 162.158.186.248 08:29, 23 August 2024 (UTC)
In order to remove calculus from the scenario one needs a pressurization system that keeps Pair + Pliquid, constant at the hole. This requires sensing the height of the liquid surface and increasing the air pressure as the surface drops, the relationship depending on the density of the liquid. Mjackson (talk) 22:02, 22 August 2024 (UTC)
I wish my maths teachers back in the day had come up with any examples like this and I might have got a notion that calculus can be good for something after all, that there is an actual justification of learning it. I still might have failed in grasping it, mind you, but at least I'd have the decency to feel just a tiny little bit bad about it. I realise this is probably making me the odd one out here, but I felt I should mention it because it's linked to a fundamental problem of teaching - teaching anything at all, not just maths: most of the time you need to sell to your students the notion that knowledge and skills outside of your fields of interests, those that certainly don't relate to any career you have in mind for yourself, are valuable enough to justify the pain of learning them. You see, generations of "dumb", "lazy" students like I used to be myself have got it right on instinct: anything complex and abstract is literally painful to learn. Thinking hard in fact generally hurts, even if you pretend to yourself you like it (as I do, too, but what we really like are the results we come up with when we're done). Psychologists recently hammered this fact home in a large meta study [1] [2]). So with something as complex and abstract as calculus, you'll have to sell to them it's worth learning anyway, even despite a very real prospect of being able to live a perfectly happy and successful life without it, and if it's only of the weak basis of "it may still turn out to come in handy at some point". I'm a teacher myself, in case you're wondering, and if I taught maths and calculus and suchlike, transferring to it the same "signature" hands-on approach I'm somewhat known for using in geography, it'd be quite possible you'd see me drill an actual hole into an actual barrel (and likely make a show of installing a tap to make it reusable, too). PaulEberhardt (talk) 10:21, 24 August 2024 (UTC)
If the tank were sufficiently pressurized, they might end up having to mop up careless calculus teachers. The Hydraulic Press Channel has a series of videos showing the results of fittings popping off of over-pressurized tanks. It did not bode well for any ballistic gel dummy heads that got in the way. These Are Not The Comments You Are Looking For (talk) 03:17, 26 August 2024 (UTC)
- Don't worry. Us teachers are professionals, because we get paid for it. 😁👍 PaulEberhardt (talk) 07:38, 29 August 2024 (UTC)
