184: Matrix Transform
| Matrix Transform |
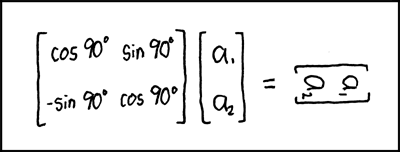 Title text: In fact, draw all your rotational matrices sideways. Your professors will love it! And then they'll go home and shrink. |
Explanation[edit]
A rotational matrix transformation (i.e. the big brackets with "cos" and "sin" in them) is used in computer graphics to rotate an image. In general, to rotate a point [a1, a2] in a 2D space by z° clockwise, you can multiply it by the rotation matrix [[cos z°, sin z°], [-sin z°, cos z°]]. In this case, the left side of the equation is rotating [a1, a2] by 90°. Simplifying the trigonometry, the 90° clockwise rotation matrix is [[0, 1], [-1, 0]], so multiplying this by [a1, a2], you should get [a2, -a1].
The joke is that the author performed the rotation transformation on the notation rather than on the vector it represents.
Rotational matrix transformations are a special case of the general linear matrix transform, which can do other things to images, including the other two affine transformations of scaling them or translating (moving) them. On a pedantic note, normally mathematics uses counterclockwise as a default, although computer graphics frequently use a clockwise default, so this may be an intentional reference.
So the title text may be referring to the professors going home (translation) and shrinking (scaling) from the joke; it may also refer to them going home and seeing a shrink (counselor) in despair of their student understanding.
The red text in xkcd: volume 0 notes that mean people wrote into state that the direction of rotation was wrong, but that's due to readers not checking the signs. Rather, the actual typo was that "shrink" in the title-text should have been "drink", but was left because of (1/2)[a1, a2].
Transcript[edit]
- [A square matrix next to a vertical two-by-one matrix, equated to a horizontal matrix that looks like the two-by-one matrix turned 90 degrees.]
- [Square matrix:
- cos90° sin90°
- -sin90° cos90°]
- [Two by one matrix:]
- [a₁
- a₂]
- [An equal sign]
- [The same two by one matrix, but rotated by 90 degrees clockwise:]
- [a₁
- a₂]
Discussion
This baby needs a bit more rigor. --Quicksilver (talk) 05:23, 24 August 2013 (UTC) 173.245.62.84 07:54, 7 April 2014 (UTC) I think this is also a reference to the movie "The Matrix", specifically the now famous scene where Neo does 90degree back bending to dodge bullets. 173.245.62.84 07:54, 7 April 2014 (UTC)
Maybe another reference: They'll go home (translation matrix) and shrink (scale matrix). Translation, scale and rotate are probably the most popular linear transformations. 108.162.218.89 23:39, 14 May 2014 (UTC)
I've been teach that the rotation was anticlockwise. Do computer turn the other way round that math teachers? by the way (left ( matrix{0 # 1 ## -1 # 0} right )*left ( binom 1 0 right)=left (binom 0 1 right) if you know what i mean. get fun. Yomismo (talk) 09:28, 18 March 2015 (UTC)
IIIII'm pretty sure the "shrink" is a typo, and he meant "drink". My evidence is the xkcd book, where he just flat-out says it.
On clockwise/counterclockwise: I think Randall is using screen coordinates (where the top left is (0,0) and the point (1,4) is one below (1,3)), instead of standard Cartesian coordinates where the bottom left is (0,0) and going from (1,3) to (1,4) means going upwards. 162.158.155.170 13:07, 17 May 2019 (UTC)
