Difference between revisions of "1282: Monty Hall"
(→Explanation: better wording) |
(fixed type (behing->behind)) |
||
| Line 18: | Line 18: | ||
===The Monty Hall Problem=== | ===The Monty Hall Problem=== | ||
:''for an in-depth analysis of the Monty Hall Problem, see {{w|Monty Hall Problem|its article at Wikipedia}}'' | :''for an in-depth analysis of the Monty Hall Problem, see {{w|Monty Hall Problem|its article at Wikipedia}}'' | ||
| − | The apparent "paradox" of the Monty Hall Problem is that many people's initial reaction once the host opens a door to reveal a goat, is that there are two remaining doors, one with a car and one with a goat; and therefore there is an equal probability the car is | + | The apparent "paradox" of the Monty Hall Problem is that many people's initial reaction once the host opens a door to reveal a goat, is that there are two remaining doors, one with a car and one with a goat; and therefore there is an equal probability the car is behind each door. many people therefore believe that switching makes no difference to the odds of winning a car. |
However, assuming that the host has knowledge of which doors contain goats, and that his choice of which door to open is always an unchosen door containing a goat, it is actually twice as likely that the contestant will win the car if they switch than if they keep their original choice. This is because the contestant initially had a one-in-three chance of choosing the car (and a two-in-three chance of choosing a goat). Switching always wins the car in those two-thirds of cases where the contestant initially chose a goat. The probability of winning by switching is therefore the same as the probability that the contestant initially choose a goat. | However, assuming that the host has knowledge of which doors contain goats, and that his choice of which door to open is always an unchosen door containing a goat, it is actually twice as likely that the contestant will win the car if they switch than if they keep their original choice. This is because the contestant initially had a one-in-three chance of choosing the car (and a two-in-three chance of choosing a goat). Switching always wins the car in those two-thirds of cases where the contestant initially chose a goat. The probability of winning by switching is therefore the same as the probability that the contestant initially choose a goat. | ||
Revision as of 16:14, 25 October 2013
| Monty Hall |
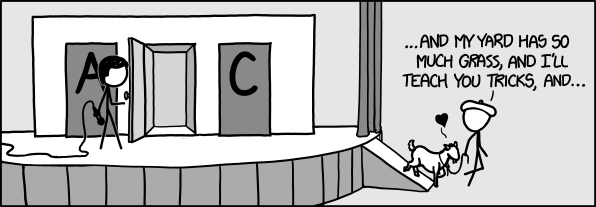 Title text: A few minutes later, the goat from behind door C drives away in the car. |
Explanation
This comic is a reference to the Monty Hall Problem, a probability puzzle based on the US game show 'Let's Make a Deal' and named after its original host, Monty Hall. The premise of the show was that Hall would offer "deals" to contestants pulled from the audience in which they could win cash and prizes. Some deals involved games/tasks the contestant had to perform, while others simply involved the contestant making choices between a series of doors or boxes. In such games of choice, there were often several prizes and typically at least one "zonk": The show's name for an undesirable "gag" prize, which on the original Monty Hall version of the show were frequently animals such as goats.
In the classic version of the Monty Problem, a contestant is offered a choice of three doors. Behind two doors is a goat, and behind one of them is a car. First, the contestant chooses a door, which remains closed. The host then opens one of the two remaining doors and reveals a goat. The contestant is then offered a final choice of whether to switch his pick to the remaining closed door, or keep the door they original chose. The problem involves an analysis of the the probability of the contestant choosing the car given certain circumstances.
The problem (as does the game show) assumes that a contestant would want to win a car, and would be disappointed to win a goat (a zonk), which most contestants would have no ability to house, and no use for. The comic shows that Beret Guy, upon the host revealing that door B has a goat behind it, chooses to take the goat to keep as a pet, which makes them both very happy.
The title text references the car and the remaining goat, untouched behind the remaining doors.
The Monty Hall Problem
- for an in-depth analysis of the Monty Hall Problem, see its article at Wikipedia
The apparent "paradox" of the Monty Hall Problem is that many people's initial reaction once the host opens a door to reveal a goat, is that there are two remaining doors, one with a car and one with a goat; and therefore there is an equal probability the car is behind each door. many people therefore believe that switching makes no difference to the odds of winning a car.
However, assuming that the host has knowledge of which doors contain goats, and that his choice of which door to open is always an unchosen door containing a goat, it is actually twice as likely that the contestant will win the car if they switch than if they keep their original choice. This is because the contestant initially had a one-in-three chance of choosing the car (and a two-in-three chance of choosing a goat). Switching always wins the car in those two-thirds of cases where the contestant initially chose a goat. The probability of winning by switching is therefore the same as the probability that the contestant initially choose a goat.
The switch essentially gives the contestant both remaining doors instead of just the one door originally chosen. Because the host always has at least one "goat-door" available to open, the fact that the host reveals a goat does not provide the contestant any new information about their initially chosen door. The inital door still has a two-in-three chance of being a goat, and switching still has a two-in-three chance of winning. Opening a goat-door simply shifts all of the probability of the remaining two doors being a car to the remaining unchosen door.
There has been great debate about the precise wording of the problem, and what assumptions or rules might apply. Variants of the problem have the host open one of the two remaining doors at random, which could result in the car being revealed, and the game ending. In that scenario, if a goat is revealed, there is in fact an equal probability of winning by switching or keeping the initial door.
Transcript
- [A game show presenter is standing in front of three doors, the left door labeled "A", the right door labeled "C", and the middle door presumably labeled "B". The "B" door is open. Beret Guy is walking away with a goat.]
- Beret Guy: ...And my yard has so much grass, and I'll teach you tricks, and...
Discussion
This has absolutely nothing to do with "The Monty Hall Problem". It's strictly about the TV game show Let's Make a Deal. In the game, contestants are often given a choice of several options (Curtains, boxes, envelopes etc). Generally, one has a valuable prize (such as a car), and the others either have a lesser prize or nothing. The "nothing" prizes are often given a colorful name, such as "A pig in a poke". Colloquially, such losing prizes are known as "winning the goat". The joke here is that the contestant, having lost the car, is happy to get a goat as a pet. (In fact, the fine print of the rules make it clear that contestant do not really get such "losing" prizes) JamesCurran (talk) 15:21, 25 October 2013 (UTC)
- I believe this is correct. The focus of this comic is that he didn't win the prize, but instead got the gag prize. Most contestants on the show are bummed out, but Beret Guy is actually excited for a new pet goat! Sucks though that you can't actually keep the goat like the above commenter said. Uctriton00 (talk) 17:41, 25 October 2013 (UTC)
- You cannot say it has nothing to do with "The Monty Hall Problem" when the title of the comic is "Monty Hall" and the "winner" is leading away a goat. What? Randall sidestepped expectations by not dragging us through the Monty Hall problem again? This sounds like the type of misdirection that you might find in a...joke! Zounds! 108.162.219.58 23:21, 4 February 2014 (UTC)
Monty hall. Is this a Monty Python reference? Or something related to a skit of theirs'? --Commarchinin (talk) 04:18, 25 October 2013 (UTC)
- Not a Monthy Python -- Monty Hall is a game host famous for Let's Make a Deal which gave birth to the Monty Hall Problem Spongebog (talk)
I don't understand "It is known that door 3 has a goat, but nothing else." What do you mean by that? At the beginning in the Monty Hall problem, a contestant knows nothing. --209.51.184.11 04:27, 25 October 2013 (UTC)
It goes like this: Player chooses door A, Monty then opens a door he knows there is a goat behind. Player is then offered a chance to switch.
If you do not switch you get a 1/3rd chance of winning because it was a 1 in 3 guess and nothing changed. But if you take into account that Monty will ALWAYS open a goat door and never a car door you can recalculate the odds. So you have a 1/3rd chance that you initially chose the car which means you will lose if you switch 1/3rd of the time, but you had a 2/3rd chance of not selecting the car initially meaning you have a 2/3rds chance if you switch at winning the car. 184.66.160.91 04:58, 25 October 2013 (UTC)
- Reminds me a bit of 1134: Goats make sense. Goats are fine. --132.230.1.28 08:39, 25 October 2013 (UTC)
Goldstein-Izayoi (talk) 14:53, 25 October 2013 (UTC) Umm, I think there's no telling if the Beret Guy chose A or C in the beginning~
- It's either A or C. Then the player should choose again between A or C. Xhfz (talk) 14:56, 25 October 2013 (UTC)
- Sequence of the events (assuming Beret Guy initially selects door A)
- Monty: Pick a door.
- Beret Guy: I choose A.
- Monty: I will open another door. It is B. (He opens it and they see a goat). Do you want to switch doors? (Meaning if he will switch from A to C.)
- Beret Guy: I choose door B.
- Beret Guy (to the goat): ...And my yard has so much grass, and I'll teach you tricks, and...
- A few minutes later, the goat from behind door C drives away in the car that was behind door A.
"In that scenario, if a goat is revealed, there is in fact an equal probability of winning by switching or keeping the initial door." I'm not sure of this, can anyone explain? It seems to be stating that simply because of the random chance of the host picking the goat door in this situation then the facts about probability change.This seems to be a very large stretch. Surely in this situation since the host is picking randomly then your probabilities of losing are increased but the moment he does randomly pick a goat door then your chances of winning by switching remain the same as they were in the original problem, 2/3. --Lackadaisical (talk) 17:29, 25 October 2013 (UTC)
- Let's see... for a "random door opened by host", split it as follows: Initial choice is G (2/3rds goat), or C (1/3rd car). If G, then host has even chance of getting a goat, GG (2/3 * 1/2 = 1/3) or a car, GC (2/3 * 1/2 = 1/3), whereas if C then host has 100% chance of a goat, CG (1/3 * 1 = 1/3). A GG happens at a frequency of 1/3rd (best to swap), a CG happens at a relative frequency of 1/3rd (best to stick) and a "game ender" happens for the final 1/3rd (no choice, no win). Thus in any non-ended game (i.e. excluding the car-revealing third of possibilities), you have equal chance regardless of what you do.
- You can also analyse it explicitly by noting down the full six combinations of "Goat 1", "Goat 2" and "Car" in the "First chosen", "Host chosen" and "Swap choice" doors. "Swap choice" is the winning move in two circumstances (having sequentially had "G1 then G2" or "G2 then G1") and "First choice" is the winning move in two others ("C then G1" or "C then G2"), with the two remaining (G1,C or G2,C) being end-games that make the option moot.
- Note, the above frequencies only happen with the 'dumb host'. Re-run it with a 'knowing host' and you get your proof for the "best to swap" scenario. (I found the above explanation by 184.66.160.91 to be the most succinct explanation of this problem that I've seen, BTW. Although maybe I have the advantage of understanding it in the first place.) 31.111.43.68 00:36, 26 October 2013 (UTC)
I agree with the various comments above. While this comic does use a goat, it really isn't making use of "The Monty Hall Problem" at all. That involves offering a player a chance to switch doors, and there's no indication that happened here. In this comic, for all we know, Beret selected door B, won a goat and, unlike most players, was pleased with having won a goat.
Even if one were to assume the Month Hall Problem scenario occurred, Beret isn't following it. That scenario involves the player being offered a choice between keeping their original choice (a door currently closed) or switching to the other still closed door. Choosing the door that was opened is not part of the Problem. So if Beret was being offered the Problem choice, he took neither of the options offered to him. 67.51.59.66 20:38, 25 October 2013 (UTC)
I remember the show, in Monty's day, vaguely. The deals varied but I don't think there were ever two goats. Typically I think there was a big prize such as a car, a moderate prize like a washer/dryer, and a zonk. Player chose a door, Monty revealed another door that had the washer / dryer, to show the player that it was now 50/50, car or nothing. He might ask if he wanted to switch to the unchosen, unopened door, or switch to the open door and go home now with the washer / dryer. OR he might offer him cash. "I'll give you three hundred dollars to walk away now. No? How about five hundred dollars?" The car might have been worth $3000 or something, so if you don't feel lucky, you might take a sure $500 instead of a 50/50 shot. Wrybred (talk) 21:53, 25 October 2013 (UTC) wrybred
Observe that in the comic only one of three doors is open. The second door was never revealed. The reason why this joke is funny is because the contestant (Beret Guy) subverts the playing rules by not choosing a second door and therefore disregarding the possible car and leaving happily with the goat that was revealed in the first phase of the game:
- "There's a goat behing door B! Now you must stick to your door A pick or switch to door C..."
- "Nah... let it go. I take the goat!"
- "But, but, you must choose a second door..."
As for all of you who say it's about Let's Make a Deal and not The Monty Hall Problem, keep in mind that xkcd is a comic about nerdy-ness stuff. Keep in mind also that outside the USA people have rarely heard of Let's Make a Deal but most people who went through undergrad-level Probablity Theory heard about the Monty Hall. 83.41.36.244 02:53, 26 October 2013 (UTC)
In Victor Hugo's Hunchback of Notre Dame, the main characters are in a conflict over the love of Esmarelda, while the character of Pierre Gringoire falls for her goat (Djali). I think Beret guy here is like the poet and playwrite Pierre Gringoire. 17:03, 26 October 2013 (UTC)
The title says: Monty Hall – so it is of course to do with him… It is in the comments above that The Monty Hall Problem is mentioned. The funny thing is that if the Beret guy fails to comply with the rule of the quiz show, then Monty Hall do have a problem… :)
(By the way - the Beret looks a lot like the optimist in the What if explanation - Glass Half Empty - is this interesting enough to be mentioned in the trivia section) Kynde (talk) 09:30, 28 October 2013 (UTC)
This comic reminded me of the lamb scene in The Little Prince. I feel like Randall put it in intentionally. Thoughts?Deyesed (talk) 00:39, 1 November 2013 (UTC)
