1882: Color Models
| Color Models |
 Title text: What if what *I* see as blue, *you* see as a slightly different blue because you're using Chrome instead of Firefox and despite a decade of messing with profiles we STILL can't get this right somehow. |
Explanation[edit]
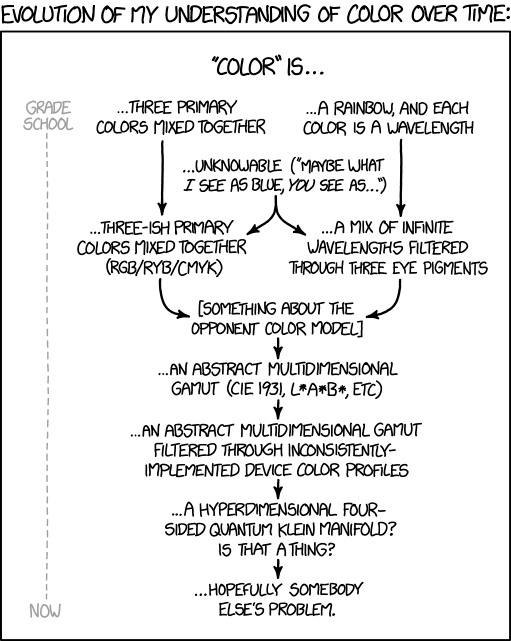
Randall is describing how his level of understanding of colors has changed by age. The chart starts with two tracks of understanding color.
In grade school he learned about the primary colors, and the very simple model of colors, as shown in the left track. Mixing of color solids, as in painting (or finger painting being probably the earliest exposure to color mixing), is intuitive for a child. The process is subtractive, and the more colors you mix the darker and closer to black you get. Color is seen by the eyes when light bounces off the solid colors and becomes light of different wavelengths that the eye can then see. However at this level, things just "look" like different colors without understanding light's role. The color models mentioned in the second point of the left track are the additive model RGB (red-green-blue) and the subtractive models RYB (red-yellow-blue) and CMYK (cyan-magenta-yellow-key, used in color printing).
The right track is about mixing of colored light, as in prisms and light waves, where mixing colors is additive and the more you mix the lighter and closer to white you get. But this is without a real understanding of light bouncing off surfaces, and is limited to an understanding of different colors of light and how they mix. The first exposure in grade school is usually by shining white light through a prism to separate it into the different visible colors.
Meanwhile, philosophically, color is unknowable because it's impossible to say if everyone has the same qualia for colors. E.g. "Maybe what I see as blue, you see as my idea of purple, but we both call it blue because we've been brought up to know to call that color blue?."
The opponent color model connects these two models, by considering how the signals from rods and cones are processed, after different wavelengths of light are absorbed by different rods and cones in the eyes.
The "complex multidimensional gamut" mentions two more models: CIE 1931 and L*a*b*. These are more detailed models based on the opponent color model, which precisely define how a particular color maps to the different channels that our eyes see.
However, understanding how the eye sees color still isn't enough, because not every device can display all the colors your eye can see. Your laptop might have a different gamut from that of your phone, and when you print the page, you might see yet another color. To handle this issue, web browsers use "color profiles", so that an image can be tagged with the color space it uses and the browser can handle it appropriately. Unfortunately, browsers do this inconsistently and not very well.
Further complicating the matter, ostensibly identical device may show colors differently (depending on how they are adjusted, variations between devices, aging of the device, and the viewing environment). Devices and software exist to attempt to match systems to reproduce colors consistently, however most systems are not set up this way, color correction can be complicated, and the corrections have to be frequently readjusted.
The "hyperdimensional four-sided quantum Klein manifold" is a joke, and could also be a pun upon the color Klein Blue. A Klein manifold is described by the Klein bottle, where the bottle was originally a surface (a mix-up of the German words Fläche for surface and Flasche for bottle). It is a two-dimensional manifold, or simply just a surface with some special characteristics. Randall is here projecting an "abstract multidimensional gamut" onto an even more complicated surface, presumably in order to eliminate the errors in color rendering caused by previous attempts to eliminate the errors in color rendering. The Klein bottle has to be projected into 4 dimensional (4-D) space for this to work, as it would otherwise intersect with itself. The “quantum” may be a reference to the "color" charge in Quantum chromodynamics.
Eventually it appears Randall has given up, realizing color is very difficult and hoping somebody else will deal with the difficulty in describing, understanding and using the concept of colors.
The title text expands on this joke, implying that the reason for the "unknowable" answer in the comic is that everyone's browser shows colors slightly differently. Despite the complexity and thoroughness of color models, this common software can't get it right.
Transcript[edit]
- [A simple flowchart is shown. The text above the panel reads:]
- Evolution of my understanding of color over time:
- [On the left side is a vertical dashed line in gray, on top it's labeled:]
- Grade school
- [And at the bottom the label reads:]
- Now
- [Header above the chart:]
- "Color" is...
- [The chart starts with three items, one left and an other on the right, a third is below in the middle.]
- ...three primary colors mixed together
- ...a rainbow, and each color is a wavelength
- ...unknowable ("maybe what I see as blue, you see as...")
- [Arrows from the left and the middle item point to a new left one, while two other arrows from the middle and the right item lead to one at the right.]
- ...three-ish primary colors mixed together (RGB/RYB/CMYK)
- ...a mix of infinite wavelengths filtered through three eye pigments
- [The arrows of both items point to one in the middle:]
- (something about the opponent color model)
- [The remaining items are all in the middle and each is connected by one arrow downwards to the next.]
- ...an abstract multidimensional gamut (CIE 1931, L*a*b*, etc)
- ...an abstract multidimensional gamut filtered through inconsistently-implemented device color profiles
- ...a hyperdimensional four-sided quantum Klein manifold? Is that a thing?
- ...hopefully somebody else's problem.
Discussion
For those who want to know a bit more about color, this site is a good start. Zmatt (talk) 15:08, 28 August 2017 (UTC)
This comic shows the trend of having a simple and satisfactory explanation for something, and the exasperation with repeatedly realizing the inadequacy of the explanation, making revisions, and having a more complex yet still inadequate model.
As Randall began his schooling, he learned that mixing the primary colours of pigment (red, blue, and yellow) together he could create almost any colour, so colour must be a combination of those 3 colours.
He also learned about rainbows, and that the colours in the rainbow were just different wavelengths of light. Somehow these different wavelengths created unique colours.
As Randall got older, philosophy and a discussion on perception came into play, and Randall came to the realization that his experiences are analogous to but not necessarily the same as his peers.
As he got older, Randall learned about colour spaces as used in pigments, light, and printing, possibly from computer science (Red, Green, Blue; Red, Yellow, Blue; Cyan, Magenta, Yellow, Key) as well as the physics of electromagnetic rays and the biology of vision, understanding that visible light is a small portion of the electromagnetic spectrum - one crudely interpreted by the 3 types of cones in our eyeballs.
Randall then learned about the opponent process model, wherein the signal from cones are not interpreted individually, but in difference to one another. "Responses to one color of an opponent channel are antagonistic to those to the other color. That is, opposite opponent colors are never perceived together – there is no "greenish red" or "yellowish blue"." (from wikipedia)
After that, Randall comes to understand the modeling of colour spaces and the design and limits of human visual perception - despite only having three cones, color space cannot be made into a triangle and still cover the gamut of human colour experience.
Klein manifolds are beyond me, you'll have to fill in something about that.
Eventually, the modeling becomes so complex (and yet still unsatisfactory) that Randall hopes it becomes someone else's problem. 108.162.238.5 15:50, 28 August 2017 (UTC)MagnusVortex
I'm familiar with klein manifolds, they're peculiar 4D dimensional topological objects related to mobius strips. I have no Idea how they might relate to color, and doing a search for "a hyperdimensional four-sided quantum Klein manifold" returned pictures of bicycles...
It might be good to point out in the explaination that he progresses from a dual nature of color (light, and paint) at the beginning and then trends to a unified explaination of color. 172.68.142.179 18:27, 28 August 2017 (UTC) Sam
- Yes those are great looking bikes and are called Klein Quantum racing bikes... so Google did its job of keyword matching. Rtanenbaum (talk) 20:40, 28 August 2017 (UTC)
- The beauty of explainxkcd
The explanation of this comment is a great example of why this site is delightful — and nigh-invaluable! Thanks, regulars, for doing the work to help us understand all this. 108.162.246.101 (talk) (please sign your comments with ~~~~)
Text explanation
I think the explanation of the text is missing an important point. It starts like it's about the philosophal question of "the same color for everybody", but ends with a very mundane explanation, which I think quite funny.
141.101.69.9 21:18, 28 August 2017 (UTC) Loïc
Yes, the description needs to include the fact that the top reference to color being unknowable is a reference to qualia. The brain of one individual may interpret colors differently than the brain of another individual, but since we would all use the same words for our interpretations of the same wavelengths, we can't really know if how I see blue is the same as how you see blue, hence that reference. But then in the tag, he has swapped out the reason for our different interpretations for the same color, blaming our browsers instead of our brains.
DarkJMKnight (talk) 11:14, 29 August 2017 (UTC)
Exactly this. Although really that only relates to our experience of colour, so I'm not sure how much relevance it has to the colour mixing track, despite the arrow. 141.101.98.106 13:11, 29 August 2017 (UTC)
I added a comment about qualia, which could probably be improved upon. --172.68.47.66 14:52, 30 August 2017 (UTC)
"As the 4th dimension is time, the color space would probably change all the time."
...no. No. I'm removing that. Just... no.
Hakr14 (talk) 23:03, 28 August 2017 (UTC)
- Just to explain to the people that aren't engineers, physicists, or mathematicians; while "the three dimensions" are commonly thought of as height/width/depth, with time often used as the 4th dimension, there is nothing that requires "dimensions" to refer to those properties. For example: a flat plane with a temperature distribution could be said to have three dimensions (height/width/temperature), or a cube could be said to have four (height/width/depth/temperature)108.162.237.100 17:00, 6 September 2017 (UTC)
Isn't the title text a reference to that pretty old Chromium bug? 162.158.22.4 13:53, 29 August 2017 (UTC)
I don't think Randall even scratched the surface. Ask "What is Yellow?"...it's the almost pure frequency of light given off by a sodium lamp at 589nm wavelength. Then, take a digital photo of a sodium lamp and look at the picture on an LED monitor. The color looks the same...but now you're looking at a mixture of red and green LED's - so you're seeing two frequencies at 660nm and 530nm...there is no yellow light. So, you ask yourself - is it the case that mixing two frequencies that the eye can see creates the illusion of a colour between the two?
Well, what color do you see when you mix red and blue? Magenta...right? But what color is midway between red and blue? That's Green. So the difference between Magenta and Green *should* be about the same as the difference between "Sodium lamp yellow" and "Picture of sodium lamp yellow".
The Mantis Shrimp can see 12 'primary colors' and is sensitive to the plane of polarization of the light. We see 3 primaries and have no clue about polarization.
- That's not true. We can see Haidinger's Brush. See https://en.wikipedia.org/wiki/Haidinger%27s_brush . 198.41.238.34 10:09, 30 August 2017 (UTC)
Humans are all essentially color blind. SteveBaker (talk) 16:55, 29 August 2017 (UTC)
There is no mention of the RGB/RYB/CYMK issue in the explenation 162.158.111.211 06:13, 30 August 2017 (UTC)
What if, what you see as blue when you look at the sky in real life, I see as a slightly different blue, because the different web browsers we've been using have retrained our eyes to perceive meatspace differently? Promethean (talk) 20:57, 2 September 2017 (UTC)
For what it's worth, the most natural way to describe color exactly is as an infinite-dimensional Hilbert space. Each pure frequency is a dimension, so a color is a vector with |R|-many elements, each representing the intensity of a different frequency. The inner product induces a norm that represents the brightness of the color. The sensitivities of the cone cells are basically encoded in the definition of the inner product. 108.162.237.59 20:01, 26 August 2022 (UTC)
- Depends on what you mean by color. I don't think eyes (or digital sensors) can perceive an infinite range of frequencies. Referring to high-energy gamma rays as "colors" and then trying to distinguish between colors based on their energy difference would be to distort the meaning of the term. Same for radio at the other end. Even in the visual range, can the eye distinguish between 660nm and 660.1nm light? I very much doubt it. In any practical sense, then, there are not "infinite" colors. Nitpicking (talk) 12:52, 7 January 2023 (UTC)
- I'm not sure what the qualification is for "colour", but if it's based upon a particular sensing creature/aparatus, then there is a degree of finiteness tied to how many chromatic detection ranges it employs (and the response curve each is informed by, and then further by the perception resolution of the near neighbouring frequencies). It could be quite tight, and it would be fully calculable if it involved digital encoding (less sure in analogue scenarios and, e.g., human vision is tricksy... as can be seen in the Checker shadow illusion, and similar) so properly finite. Even for a given hyperspectral camera.
- But if you want to cover [i]any[/i] observation(/-device) that can be made then you're effectively unbounded by the possibilities of 'spectral resolution'. Can your eye differentiate between 660nm and 660.1nm? Probably not. But you cannot say that no eye does (and we can and do build sensors that would do so).
- Possibly physical laws intervene at one point though. Effectively a "Planck spectral-separation", as the limited number of elements compounded into a (very large but still finite...ish) number of receptive materials, setting an upper bound of direct response to bits of any spectra. Or, if prism-split and projected, the limit to which the resulting smear of rainbow light can be spread out and then having the limit of assessing a thin enough wedge of it. But, with always the possibility of finding a trick to go beyond the current level chromatic differentiation (applying an oscillating reflector, LIGO-like, to alternate the very slightest red-/blue-shifts back and forth across the existing threshold in a detectable way?), its as near as dammit an infinitely detailed continuum, probably even beyond what useful detail might be usefully presented by the otherwise sane bit of the universe that is blithely transmitting whatever light we are so interested in receiving for analysis. 172.71.242.140 16:08, 7 January 2023 (UTC)
 Add comment
Add comment
