2465: Dimensional Chess
| Dimensional Chess |
 Title text: In Dimensional Chess, every move is annotated '?!'. |
Explanation[edit]
Being good at chess is often regarded as a sign of high intelligence. A skilled player must be able to consider possibilities several moves in advance, which can be represented as an exponentially growing tree of possibilities. The branching factor of chess, the approximate number of legal moves available at any given time, is about thirty-five, although most players (human and computer) will use heuristics to prune the trees to regard only likely or promising moves. Expanding the playing field by generalizing to three-dimensional chess (or beyond) will increase the branching factor even further, and so someone who is able to competently play three-dimensional chess could be regarded as even more intelligent than someone who can only play two-dimensional chess. Making chess into an N-dimensional game thus makes it arbitrarily more difficult, even before Randall's addition of non-uniform dimensionality of the board.
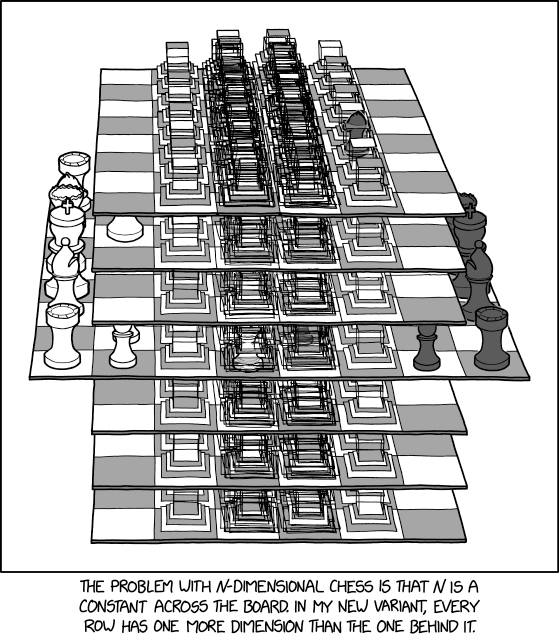
Regarding Randall's rule that "every row has one more dimension than the one behind it," it is easiest to see how this is applied with the first two rows on each end. The first row on each end is a like a row on a traditional two-dimensional chess board (albeit played with three-dimensional pieces): you can go from left to right, or forward into the next row. The second row then becomes a two-dimensional row of a three-dimensional space: you can go left to right, forward to back, and now top to bottom. Note that there are seven spaces (represented by "shelves") from top to bottom, as opposed to the typical eight rows from left to right/front to back. This is likely to make sure there is symmetry between how many additional spaces are on top versus on the bottom (three, in this case). Moving another row would presumably add movement in some other direction to make it more complicated/interesting. This escalates until somehow the middle two rows require moving pieces in five dimensions (the middle two rows are four-dimensional rows + moving to other rows as fifth dimension), despite humans only being able to experience three spatial dimensions.[citation needed] This could potentially be accomplished via playing on a computer, such as in the game 5D Chess with Multiverse Time Travel.
There are eight squares on the first row, 56 on the second row and presumably 504 on the third and 1512 on the fourth, thus making the total number of squares 4160 rather than the 64 of a traditional chess board. The drawing shows apparently five squares (or boxes) stacked on the third row and if this is also formed symmetrically, there are four hidden out of sight. The middle rows are already quite convoluted but it seems as if Randall drew three boxes along this dimension. Due to this dimensionality increase, there is plenty of free space in the middle board, drastically changing the game dynamics such that shadowing plays very little role and that movement is very unrestricted.
The title text refers to the practice of writing down what happens throughout the game, so that it is possible to review how the game progressed later. Recording moves in this fashion is required in most tournament situations. There are several common forms of Chess notation used for this purpose, and as well as indicating the moves, players may add annotations indicating their opinions about whether a particular move was good, bad, or peculiar. According to the title text, every annotation is followed by "?!"—which indicates a questionable move, of dubious value but not obviously a blunder either. The joke is that the variable-dimensional game is so complicated that any move will answer this description.
There appears to be the normal chess pieces (so no Fairy chess pieces), but the game has already started (there are white and black pawns in one of the middle squares, and both white and black knights have moved.
Note that "in dimensional chess" may be a pun on "N-dimensional chess."
Transcript[edit]
- [A chessboard is depicted in the middle of a stack of boards. All pieces visible on the middle board are in their starting positions, except the white knight from a2 at d1 and the black pawn from g2 at e2. There are three boards each above and below the original, missing columns a and h. On columns c & f on each board, there are clear cubes with a small pedestal on each square. Columns d & e are similar, except with multiple cubes on each square. No chess pieces are visible, except for a white piece -- not clearly visible, but implicitly the white king's knight -- on the second board above the middle on b2 and a black pawn on the top board on f3. Below the chessboards is a caption]
- [Caption below the panel]:
- The problem with N-dimensional chess is that N is a constant across the board. In my new variant, every row has one more dimension than the one behind it.
Discussion
How best to describe the addition of dimensions? The admirable first author goes as far as the second row, but there appear to be more... ahem... 'depths'. The first is 'sideways', though from this non-playing angle it's depthways; the second adds verticality; the third initially looks to be '4d represented in 3d' perspective (now further represented in 2d, by perspective method), but the sole cube atop confuses me; the fourth is... busy... and seems to go with a hyper(hyper)cubic continuation. 141.101.99.161 18:05, 19 May 2021 (UTC)
not quite what is demonstrated in the comic but there is a game called 5 dimensional chess with multiverse time travel --172.68.57.189 19:00, 19 May 2021 (UTC)
- I don't like that game, entirely because it's called 5-dimensional but actually only has four dimensions. --141.101.98.94 06:20, 22 May 2021 (UTC)
I think this would require 5 dimensions rather than 4 as the middle rows are 4d slices of a 5d space just as the second row is a 2d slice of a 3d space 172.69.35.193 20:23, 19 May 2021 (UTC)
- I see it as there being a basic 1D between the opponents. On the Nth row away from you (on your half of the board) there's an additional N lateral dimensions. Row 1, sideways (8 columns). Row 2, sideways and up/down (7 levels). Row 3, those plus some form of superimposition indicated by scale/perhaps a sub-gridlevel elevation (6 of these?). Row 4, all those plus ??? (gonna assume 5). (...Row 5=Profit?) 162.158.158.131 22:25, 19 May 2021 (UTC)
Is there an error on the top board of this image? If I look at the sequence of squares on the vertical, they alternate black/white except for the top board. Even if I were missing some aspect of the logic, I feel like there should be some symmetry between top and bottom. 108.162.221.70 20:52, 19 May 2021 (UTC)
- Agreed, there appears to be an error.--162.158.75.220 17:18, 22 May 2021 (UTC)
Note that white made a horse move on the left side of the board, forward one and up two 172.68.57.189 21:11, 19 May 2021 (UTC)
- LOL it's called a knight. 162.158.75.221 06:08, 21 May 2021 (UTC)
- There's at least one black piece on (its) row 3, possibly a knight, and both players have at least one of their pieces on (their) row 4. There are four obvious white pieces forward of the two starting ranks (with no obvious sign that these are established starting positions in this esoteric board*) so there may be a third black piece out there, obscured from clear view. Or more likely that black Knight's movement (two squares forward, three up, one sideways and 0+ squares in the fourth-way direction) is multiple moves (2f1u then 2u1s would be the most simple projected moves).
- OP could simply be an Italian person who doesn't speak English very well. The knight is called "cavallo" (horse) in Italian. The pawn is the "pedone" (pedestrian), the bishop is the "alfiere" (standard-bearer) and the rook is the "torre" (tower).
- (* - The starting ranks appear to be as per 2D chess, with white's far bishop no longer in starting position, but if that's the one now in the nearest start-level 4th rank then it must not have made just one single 2D-like bishop's move to get there, nor is it obviously a pawn brought forward (2f starter then 1f second move, with or without an en-passant), so it may not be quite so simple, or else we've seen more than 4 white moves (and 3/4 black ones). Or both plus some possible exchange of pieces already.) 162.158.158.131 22:25, 19 May 2021 (UTC)
I interpreted the comic as the first row is normal chess- 2 dimensional. The second row starts the boards above and below- 3d. The third row would be 4d, and the 4th row would be 5d. ----
Pretty sure this is just funny commentary on people making more and more complex variations of chess, Quantum Chess, 4D Chess, 5D chess with time travel etc... but part of me looks at this and goes "that could be a real game... that could actually be a good game." just me? 108.162.221.20 21:35, 19 May 2021 (UTC) Sam
Looking at this, I note that there seems to be an assumption in the explanation that n-dimensional chess means chess with an unlimited number of dimensions. I believe that what Randall was actually saying with the "N" was "any number N", not "all numbers N together", i.e. "The problem with 3, 4, 5, 6, ... , N dimensional chess is", and that his objection is that you always only get one number for N. His board, of course, is designed to give you as few as two dimensions up to five dimensions available for any particular piece depending upon the row.
True n-dimensional chess, where there are an unlimited number of dimensions, would probably be unplayable by any Turing machine, including, of course, humans. Geek Prophet (talk) 23:58, 19 May 2021 (UTC)
- If you have an infinite number of dimensions to work with, there is a straightforward means for a king to escape forever - just alternate linear moves with diagonal moves, always away from the opposing pieces, and always along a dimension not previously traversed (there are an infinite number of these, so always one more). Any opposing piece will be one dimension behind, at the very least. 108.162.237.4 01:45, 20 May 2021 (UTC)
- That surely only works if you don't end up stuck in an infinitely-dimensioned corner (infinite dimensions but still finite+nonwrapping extent in each dimension).
- I'm not sure if there's a foolproof way not to find yourself in that corner, by evading through heretofor unused dimensions strictly around the centre of the board (where a finite number of pieces may not be able to coordinate an all-sides trap) but once there a single infinitely-dimensional queen moved one square away from all the relevent edges, protected by some handy rearward piece, could force the endgame.
- If the king itself is in that one-space-out position (not yet immediately restricted by the edge, any edge) I think it can still be considered corralled by a suitably-placed finite smattering of sufficiently-positioned (for their respective powers of projection) pieces, so even if the centre squares are freely dodgable round (which they might not be, if the opposing king is already safely stationed there, denying 3x3x3x...3 spots to the victimised king) there's a potential to be tactically/psychologically forced towards a definitely entrapping position the moment you stray towards any edge.
- (If the queen/etc is '≤2D in movement, like a 2D queen except throughout the ∞D of choice' (i.e. confined to a planar diagonal), then it may be less potent for a given distance and not be able to project a no-king-may-pass barrier even without confounding pieces, so might not be the key to the corner-shoving tactic. But then the king would surely be 'choose your single plane' too, in the moves available in its attempt to escape.)
- Boundaryless arenas (including wrap-around finite boards, or at least 'only' 8∞ in their infiniteness) might well be trivially always in an escapable position. But I have my doubts even about the fully-wrapping version, as the attacker's 'left behind' pieces may be considered significant danger again as they are then actually ahead of any king's fleeing move, and the question now is whether the king can still dodge ever-'sideways' against a concerted and sufficiently analytic opponent still with enough (2? 16? However-many-you-can-initially-start-with-on-such-a-board?) pieces of the right kinds.
- That said, whatever my proficiency with dimensional projections, I'm definitelt rubbish at chess in its standard form. So ICBW. 141.101.98.60 09:24, 20 May 2021 (UTC)
It looks like the 3rd row adds a cube on a stack of alternating colored squares, and then the 4th row does something similar with a tesseract. It gets a little crowded, so hard to be sure. Orion205 (talk) 01:36, 20 May 2021 (UTC)
It might make sense to just add a link to chessvariants.com, since there are a surprising number of multidimensional chess variants in existence besides the aforementioned 5D chess with time travel. JakobWulfkind (talk) 02:38, 20 May 2021 (UTC)
- That site's pretty hard to navigate. Do you know how to enumerate all existing variants of chess that are infinitely dimensioned, or at least >3 dimensioned? Additionally, this is a pretty exciting topic, is there any capacity for the wiki to dedicate additional pages to it? 162.158.63.78 20:15, 20 May 2021 (UTC)
Ah yes, the Ra̷s̵̡̡̛͍̖̗͖̟̞͊̀̓̉͂̈́̇̉p̵̛̤̔̂͐͗̄̿̋͛̿͗͒͒̚͘̚̚͝u̵̞̿̒̃̾̑͒̎ṱ̶̨̧̡͍̜̙͖̣̗͙̥͈̳̱̼̫͗͊̌͑̇̆͝i̵n opening. A good choice! Also, when is someone going to make a playable version of this??? 108.162.249.74 04:58, 20 May 2021 (UTC)
I don't think the explanation really needs anything to do with intelligence. "Fourth-dimensional chess" is lingo for complexity or cunning, so I think the comic is a joke based on that phrase. 172.69.142.50 05:36, 20 May 2021 (UTC)
I was disappointed that Randall did not include two odd squares - one on either side of the board - for the one-dimensional chess starting point. Of course since he does things by rows, this would necessarily limit the number of 1D starting points to one per player - and it would break the symmetry of an 8x8x? board and make it tough to pick which piece starts on the 1D row. SteveBaker (talk) 13:14, 20 May 2021 (UTC)
- My (nearly) initial thoughts, too. Row0: Square; Row1: Lateral line of squares (7 or 9 wide, to centre?); Row2: Stacked array of squares (7||9 x 5||7?); Row 3: A cube(/tesseract-slice) of oportunities; then Row4 either Row3 from the other side or a further hyper-version (singular, or doubled with anti-Row4, leading onto anti-Row3, etc...)
- Another thought I had was that every enhanced-Manhattan step from the home-row should lead to additional spread into a new dimension - to keep that consistent arrange for the branches out from each side to 'kiss' exactly in (non-euclidean) perfect contact. As with 2D chess, any four moves away from the back row (not backwards, not the most basic sideways movement) puts you onto the opponent's half. Or make it Euclidean but then it'd be on one several opponents' 'halves'. 141.101.99.251 14:54, 20 May 2021 (UTC)
- You can probably get away with the board being exactly a 8-cube of squares; row 0 will be one square, row 1 will be 8 squares, row 2 will be a 2-dimensional mess (triangle?) of squares where each square connects to exactly two row 1 squares, and so on until row 8, which will again be a square. 9-cube works too, though rows 1 and 8 will have to consist of 9 squares instead of 8. --162.158.63.78 16:53, 20 May 2021 (UTC)
Couldn't you play some of the middle parts with components from 5D chess with time traveling and multiverses or whatever it was(forgot the name)? Sarah the Pie(yes, the food) (talk) 13:53, 20 May 2021 (UTC)
If a king can move to any other space that's the same or adjacent in any dimension, then a king on the fourth or fifth row would have 188 possible moves (80 in its own row, 81 in the other high-D row, and 27 in the adjacent lower-D row). This would probably make it near-impossible to get a checkmate in this situation. Getting trapped between a neighboring (protected) queen and a 2-steps-away king would do it, of course; and you could maybe replace the queen in that arrangement with a combination of pawns and/or bishops, depending on how those generalize; but it seems it would be trivially easy to foresee any of those traps and avoid it. So I think this game would be unwinnable. 162.158.62.95 18:45, 20 May 2021 (UTC)
- The king can't invent new dimensions if they're threatened, obviously! 20:15, 20 May 2021 (UTC)
I'm imagining a form of chess, with computer opponents, where players can add new rules so long as the rules are consistent, and there's like a public wiki of rules to draw from. I'm thinking an infinitely large board where players can invent secret dimensions and move along them [maybe in a limited manner for chess], but if observed or if a player guesses the dimension, the pieces can be found. 20:15, 20 May 2021 (UTC)
My interpretation: the outermost rows are 1D. Within them, you can only move back and forth within the row. The next rows are 2D. Within them, you can move within the row as well as up and down. The next rows are 3D. In addition to the previous moves, you can move to different levels on each square. The innermost rows are 4D. Within each square, there are two ways to move (which level and which vertical plane). So obviously I'm not counting moving between the inner and outer rows as an extra dimension, though of course you may.CityZen (talk) 23:09, 20 May 2021 (UTC)
The notation in the transcript is confusing: since we are looking at the board from the side, the front left square in the center plane should be h1. So white knight from g1 seems to be moved to (two above g2). There also appears to be a white piece in some dimension around h4. The knight from g7 seems to have managed to get into some dimension around (three above f3). --Icksehdi (talk) 09:26, 21 May 2021 (UTC)
The rules for piece movement as I know them are rooted strongly in two dimensions. How would you state them for this version of the game? 172.68.189.221
- Two main options (before getting into silly amounts of options)...
- 1) 2D moves can be taken in any 2 dimensions. Bishops go equal amounts in any two possible perpendiculars (where not blocked); Knights go 1 in one axis, 2 in another; Pawns must go forward (but may take their diagonals where allowed).
- 2) Extend to N dimensions as completely as possible (for the starting row?). Bishops can (and must) move equal amounts in every axis that applies; Knights have 1(+1,+1,..)+2 moves (or, by 2001 Monolith rules, without the squaring, 1+2+3+...etc); Pawns must diagonalise in every non-forward axis.
- Rooks, of course, likely just choose an axis (any single axis) to move along. 141.101.98.152 00:08, 22 May 2021 (UTC)
- Or 3) Any combination of (1) and (2) above (i.e. do 2 above, but you can ignore any dimensions you don't like). But with both (2) and (3) we have an interesting issue: if white starts with B(d,2,+1)?!, (i.e. the queen's bishop moves to space d2, one floor up), then we have a bishop moving from a white square to a black square.--108.162.216.152 17:39, 22 May 2021 (UTC)
- My best play is to try a variant of this for six white moves (which is a variant of the scholar's mate). N(c,3,0,0)?! N(d,5,0,0,0)?! B(c,4,+3,0,0)?! Q(f,3,+2,0)?! Q(f,5,0,0,0)?! Q(f,7,0)?! If black is not paying attention, and if I'm thinking about dimensions correctly, then this could result in checkmate.--162.158.75.94 17:56, 22 May 2021 (UTC)
- If the game progresses too far (e.g. king hiding in the middle of the board), then it appears that it will either end in a draw or never end.--162.158.75.94 17:56, 22 May 2021 (UTC)
- My best play is to try a variant of this for six white moves (which is a variant of the scholar's mate). N(c,3,0,0)?! N(d,5,0,0,0)?! B(c,4,+3,0,0)?! Q(f,3,+2,0)?! Q(f,5,0,0,0)?! Q(f,7,0)?! If black is not paying attention, and if I'm thinking about dimensions correctly, then this could result in checkmate.--162.158.75.94 17:56, 22 May 2021 (UTC)
- Or 3) Any combination of (1) and (2) above (i.e. do 2 above, but you can ignore any dimensions you don't like). But with both (2) and (3) we have an interesting issue: if white starts with B(d,2,+1)?!, (i.e. the queen's bishop moves to space d2, one floor up), then we have a bishop moving from a white square to a black square.--108.162.216.152 17:39, 22 May 2021 (UTC)
Seemingly necessary rule clarification: if a pawn can no longer move due to dimensional limitations (not blocking pieces), then it becomes a queen (e.g. white pawn moves to a position which is 3 spaces above one of the starting positions for black pawns). --108.162.216.62 18:04, 22 May 2021 (UTC)
- Question 1: how easy is it to make all your pawns into queens?--108.162.216.62 18:04, 22 May 2021 (UTC)
- Question 2: is it much easier to checkmate if you have 9 queens? As an extreme example, if white has 9 queens, black has only a king, and black's king is in the middle (high-dimensional) area of the board.--108.162.216.62 18:04, 22 May 2021 (UTC)
- Seems to me the pawn can still move then. Towards the opponents end of the board. The top and bottom of the board is not the opponents side and also not the end of the pawns ability to move. So to me this seems obviously to not be an issue. The question is if it can become a queen in any dimension when reaching the opponents side of the board. Since it can likely only go up and forward, this should be so. --Kynde (talk) 09:53, 23 May 2021 (UTC)
Is it possible Randall is just having fun with the Explain XKCD crowd. Making an extremely complicated illustration that looks legitimate but is really just random to suggest that some things are not knowable even if they seem finite and therefore solvable. I just discovered there is no equation to find the exact perimeter of an ellipse: okay, there are many, but they are just close approximations or require infinite series of calculations. NerillDP (talk) 13:08, 23 May 2021 (UTC)
- As discussed, there is a method in Randall's "madness". As far as the perimeter of the ellipse equation, note that the same is true for the perimeter of a circle. We get around it by defining a special symbol that requires either approximation or summing an infinite series (or a similarly complex calculation). 162.158.255.164 19:57, 25 May 2021 (UTC)
 Add comment
Add comment
