849: Complex Conjugate
| Complex Conjugate |
 Title text: Fun fact: if you say this every time a professor does something to a complex-number equation that drops the imaginary part, they'll eventually move the class to another room and tell everyone else except you. |
Explanation[edit]
This was the second comic with one of Randall's fun facts.
This comic is a joke on the phrase "Shit just got real", which means "something has suddenly increased in difficulty and become genuinely challenging or dangerous".
Cueball is standing in front of a board delivering a lesson, and is about to multiply a wavefunction by its complex conjugate. A wave function is a mathematical description of a quantum system which uses complex values - numbers that have both a real part and an imaginary part. Multiplying a wavefunction by its complex conjugate is a common thing to do, as it yields the probability density of where a particle is likely to be found, which is a real-valued function.
Complex numbers can be written in the form a + bi, where a is the real part and bi is the imaginary part. i is the imaginary unit, defined so that i² = -1. The complex conjugate of a complex number simply reverses the sign on the imaginary part - so for the number above, the complex conjugate is a - bi.
Multiplying the complex number by its own complex conjugate therefore yields (a + bi)(a - bi). If you multiply out the brackets, you get a² + abi - abi - b²i². The abi cancel each other out, and i² can be replaced by -1. Thus, the result is a² + b², a real number, so "shit just got real" as Cueball promised.
The title text notes that you can make this joke in class every time a calculation is performed that drops the imaginary part from a complex number, but warns that it would be so annoying that the professor will eventually find a way to have the class without you in it. Because nonreal numbers are often considered to have no physical significance, turning them into real numbers to produce a final answer is so common that this joke would quickly become tedious.
The wave function shown on Cueball's board is the time-dependent Schrödinger equation 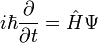 , a differential equation that the wavefunction Ψ, which determines the possible positions of a quantum particle over time, always satisfies. The derivative should be written with ∂Ψ on the top; the omission of the Ψ may be a mistake.
, a differential equation that the wavefunction Ψ, which determines the possible positions of a quantum particle over time, always satisfies. The derivative should be written with ∂Ψ on the top; the omission of the Ψ may be a mistake.
Transcript[edit]
- [Cueball, holding a marker pen down in one hand, is standing at a whiteboard with two equations, one of which is the time-dependent Schrodinger equation and the other shows what the wavefunction equals, but from there it becomes unreadable. Below is a graph with a bell-shaped curve. There are also other unreadable markings on the board below the second equation and next to the graph.]
- Cueball: Okay, anyone who's feeling like they can't handle the physics here should probably just leave now.
- [In a frame-less panel Cueball is seen writing on the whiteboard. This is seen from the side of the board, so it is just a thin line with a shelf at the bottom for putting the pen on.]
- Cueball: Because I'm multiplying the wavefunction by its complex conjugate.
- Cueball: That's right.
- [Dramatic zoom in on Cueball appears to be writing the final part of his next equation.]
- Cueball: Shit just got real.
Discussion
Actually multiplying complex number (x + iy) by its complex conjugate (x - iy) does not "remove" imaginary part, but calculate square of absolute value of complex number, (x^2 + y^2). BTW. in quantum physics the wavefunction is complex valued, and its absolute value is probability density (a real valued function). --JakubNarebski (talk) 00:57, 18 December 2012 (UTC)
I got hit in the face with my complex conjugate and lost an eye. 108.162.238.114 (talk) (please sign your comments with ~~~~)
I procreated with my complex conjugate and lost myself. 108.162.216.114 19:44, 12 August 2014 (UTC)
(a+bi)*(a-bi)= a^2-b^2 not a^2+b^2 108.162.218.142 15:48, 24 June 2015 (UTC)
(a+b)*(a-b) = a^2 - b^2 . However (a+bi)*(a-bi) = a^2 + b^2 since i^2 = -1. 108.162.219.65 (talk) (please sign your comments with ~~~~)
I think that the moving to a title text is a joke about them kicking you out of the room 173.245.50.65 20:54, 1 May 2016 (UTC)
Is it relevant that when he performs the complex conjugate multiplication, we go from a 2d image of the board to a 1d image of the board? My thinking is, that complex numbers are often used to describe a set of coordinates in 2d space. 162.158.158.233 (talk) 06:58, 14 January 2020 (please sign your comments with ~~~~)
- It might be a nice coincidence, or happened on purpose. However in my understanding and the usecases I've seen for example in electrical engineering, it was the other way round. Complex Numbers were used to describe something , e.g. phase shift, and then it could be visualized as coordinates where it was visible as a sinus-curve. (I Might be slightly wrong about the details here. It's been some time...) --Lupo (talk) 07:18, 14 January 2020 (UTC)
What's with that red text? Is that MML? ⟨Winter is coming⟩ Marethyu (talk) 21:27, 5 May 2022 (UTC)
Everyone immediately recognised how the product of a complex function with its conjugate "makes shit real" but I think there's another layer of comedy (in a sort of anti-joke way) where the complex conjugate of a real number (a+0i) is (a-0i) in other words the product of an entirely real-valued function and its complex conjugate would just be its square which is an anticlimactic turn on the joke. 172.70.93.13 15:13, 31 August 2022 (UTC)