Difference between revisions of "2701: Change in Slope"
(→Explanation) |
(→Transcript: statistics) |
||
| Line 40: | Line 40: | ||
[[Category:Bar charts]] | [[Category:Bar charts]] | ||
[[Category:Line graphs]] | [[Category:Line graphs]] | ||
| + | [[Category:Statistics]] | ||
Revision as of 18:39, 21 November 2022
| Change in Slope |
 Title text: Squinting at a graph is fine for getting a rough idea of the answer, but if you want to pretend to know it exactly, you neeed statistics. |
Explanation
| This is one of 61 incomplete explanations: Created by a SIDEWAYS STATISTIC - Please change this comment when editing this page. Do NOT delete this tag too soon. If you can fix this issue, edit the page! |
For subtle effects, such as a the slight inflection of an underlying trend, visually inspecting a graph cannot always do justice to what is there. For data on a graph, such as the scattergraph shown in this comic, the detail hidden within its cloud of points is unclear when looked at normally. The comic shows that by taking the 2D plot and reorientating it in 3D space, introducing foreshortening along the trend, the displacement perpendicular to the possibly straight line is more clearly visible.
This is very similar to more real-world activities such as polishing, cleaning and/or removing dents from surfaces, where an artisan may take an oblique view of their work, from various angles, to highlight any remaining defects that might need some attention. In mathematical terms, a graph can also be transformed mathematically to produce a squashed version (it could even effectively be the same as a 3D transform to make a 2D plot look like it is rotated in a 3D-perspective, as in the comic), although this lacks the readiness of a physical object being twisted and turned to examine it from as many angles as might be required.
Mathematics can also work with data with a further non-linear component, such as between two segments of subtly different quadratic or trigonometric fluctuation, as might replotting a non-linear dataset in a manner that transforms it into more obviously linear one (or not) by appropriate use of Log-Log graph-paper, for example. The physical equivalent of this could be to bend the paper in just the right manner to render curves as (ostensibly) straight to the observer, except for the area of incongruity, or in the case of a curved surface being worked on by a craftsman they may rotate the object (or the light being cast upon it) in a controlled manner and observe where the resulting reflections jump around unexpectedly.
The title text then goes on to say that while such a visual inspection can reveal such a quirk of data distribution, you normally still need to revert to mathematical analysis to properly quantify that quirk – such as to measure the relative likelihood of the change in trend being real, or else well within the randomness of the scattering of datapoints around any actually linear trend, and the most likely point where one gradient becomes another. The word "need" is written with three E's (as "neeed"), implying exaggerated emphasis. This may be a sarcastic way of saying that rigor is overrated when you can use tricks like this, or it may be a typo (this will become less likely as time passes without correction).
Transcript
| This is one of 32 incomplete transcripts: Do NOT delete this tag too soon. If you can fix this issue, edit the page! |
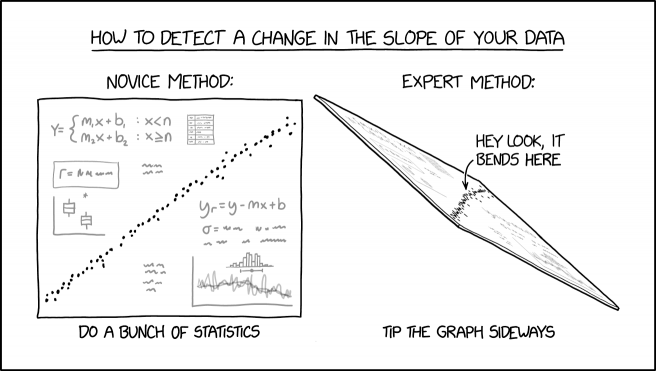
- How to detect a change in the slope of your data
- [First column, on the left]
- Novice method:
- [A graph, with dots forming a rough line, math formulas, and sub graphs]
- Do a bunch of statistics
- [Second column, on the right]
- Expert method:
- [Perspective view of the previous graph, with the legend "Hey look, it bends here" and an arrow pointing to the graph]
- Tip the graph sideways
Discussion
I am an occasional data scientist, and I can confirm this is why we have monitor stands that tilt. 172.71.94.50 16:33, 21 November 2022 (UTC)
The third e in "neeed" in the title text seems to be a typo Victor (talk) 16:41, 21 November 2022 (UTC)
- I think Randall may have added it to represent that the speaker prolongs the "e" sound for emphasis, although that's usually done with 4-5 e's. Barmar (talk) 16:53, 21 November 2022 (UTC)
- I had to double-check this, myself (presumed the 'Bot created the lage faithfully, but went straight to source to see if I needed to find a vandalism post to revert). May need a comment (to prevent hypercorrection, if not to note the implied emphisis) and certainly will if it turns out to be a typo and gets corrected (for which I'm sure a future checker will discover Randall's revisiting, but then worth a note to that effect). 172.70.90.2 17:42, 21 November 2022 (UTC)
Bender Bot was one of the main characters in Futurama. Barmar (talk) 16:54, 21 November 2022 (UTC)
- Just donning my unnecessary pedantry hat for a moment: his name is Bender Bending Rodriguez --192·168·0·1 (talk) 23:02, 21 November 2022 (UTC)
A couple(?) of authors used the word(s) "(point of) inflection", which is not really suitable for a join between two straight segments. Was tempted to talk about "discontinuity", but that really only applies to the meta-slope (derivatives, to one degree or other) where it suddenly jumps (at a point), or the derivative's derivative has jumps (as it enters and leaves the smoothly linking curve). Hope it works well enough how I left it, though. 162.158.142.176 21:28, 21 November 2022 (UTC)
For anyone curious, I used an image editor to turn the entire comic sideways and it actually does seem to work, to some degree anyway. SSM24 23:37, 21 November 2022 (UTC)
- Added; thanks! 172.71.158.230 00:14, 22 November 2022 (UTC)
- If you don't mind sharing: which program did you use? Did you tweak things like relative distance / camera FOV, to effectively select a specific point in the continuum that makes up the Dolly Zoom effect, and at the limit on one end results in orthographic projection? (Edit 10 minutes later: a better article to look at is Perspective distortion (photography)) Or did you just leave it at whatever the default is? Can you recreate the image with the two extremes, and share them? And lastly - can you upload the image (and potentially the new images) to the wiki directly, so they can be embedded in the page? Thanks! --NeatNit (talk) 17:21, 22 November 2022 (UTC)
This one shows the beauty of Explainxkcd: people reading the explanation are likely to learn accessible methods of substantial practical utility. 162.158.166.173 00:38, 22 November 2022 (UTC)
Hey, if it works for picking out lumber at Lowe’s, why not for graphs, too? - MadMarie
- There was an old bit of explanation that related it to examining physical objects (for dent/bend-removal in metalwork, I think it was) that got wiped out by a later edit. Though I'm considering my own version, now generalised to cover your experience, as it seems quite relevant/analogous to me. 172.70.90.2 14:37, 22 November 2022 (UTC)
Whoever wrote the 1st explanation needs to go touch grass and learn how real people talk, pissed me off so much I just effectively rewrote the whole thing from scratch 172.71.202.46 06:34, 22 November 2022 (UTC)
- Intrigued, looking at the first explanation (give or take that person's initial small errors/omissions) I personally find it more to the point than what it has become. Not to say the complete rewrite was wrong, but it got it not that much closer to the mythical perfection. IMO. 141.101.76.169 20:29, 22 November 2022 (UTC)
Going in a different direction than "this is silly" - if we ignore the "viewing point/parallax" issue, doing a change of basis like this is similar to linear methods like [SVD https://hadrienj.github.io/assets/images/ch12_svd/ch11_SVD_geometry.png] & PCA, and considering the graph as a mappingg in a "higher dimension" is similar to the "kernel trick" popularized by Support Vector Machines 11:31, 22 November 2022 (UTC)
Raw Data
I love this cartoon. This is definitely something that was relevant in my work!
At my old job I had some commercial or public-domain software for extracting the raw data behind a scatter plot. If anyone has something like that handy, I would love to see someone extract the data behind the graph on the left, so that we can:
1. Apply the affine transformation which generates the image on the right with the tilted paper. 2. Apply the statistical tests which Randall Munroe is alluding to.
- Knock yourself out:
| Digitized data courtesy https://apps.automeris.io/wpd/ |
|---|
0.000000, 0.015366 0.001887, 0.000000 0.002830, 0.041488 0.024528, 0.060695 0.033019, 0.014597 0.038679, 0.009988 0.044340, 0.072220 0.047170, 0.055317 0.050000, 0.072220 0.064858, 0.092964 0.070215, 0.117001 0.088207, 0.088354 0.091037, 0.122928 0.091037, 0.109099 0.100943, 0.140215 0.103773, 0.165338 0.106603, 0.178246 0.128891, 0.171331 0.147641, 0.196685 0.146226, 0.187465 0.162264, 0.215124 0.180188, 0.264910 0.182452, 0.218812 0.202830, 0.275052 0.204245, 0.261222 0.208490, 0.272747 0.217923, 0.293491 0.227358, 0.267369 0.230322, 0.234880 0.241744, 0.311930 0.256603, 0.344199 0.262263, 0.338930 0.299056, 0.376467 0.308254, 0.420261 0.313206, 0.417956 0.336791, 0.456371 0.344338, 0.433322 0.355659, 0.456371 0.367923, 0.496323 0.374055, 0.503237 0.388206, 0.503237 0.389621, 0.514762 0.409433, 0.533201 0.412263, 0.525518 0.415093, 0.540884 0.432074, 0.555328 0.446225, 0.599275 0.443395, 0.588519 0.449526, 0.537811 0.449055, 0.588519 0.468866, 0.609263 0.487263, 0.627702 0.490093, 0.636922 0.516979, 0.670727 0.523448, 0.697179 0.519809, 0.662276 0.548111, 0.697618 0.551413, 0.740642 0.550941, 0.689935 0.565092, 0.726813 0.572168, 0.724508 0.576413, 0.772911 0.582073, 0.772911 0.582073, 0.763691 0.601177, 0.785588 0.604714, 0.791350 0.625335, 0.775545 0.643394, 0.817473 0.664620, 0.855119 0.688812, 0.871693 0.688003, 0.821643 0.710374, 0.925035 0.707544, 0.806716 0.715091, 0.888156 0.717921, 0.880473 0.724148, 0.976665 0.749054, 0.927010 0.757544, 0.961913 0.763204, 0.959608 0.783016, 0.983426 0.781601, 0.971133 0.797166, 1.028756 0.802827, 1.031060 0.805657, 0.999560 0.821223, 0.966523 0.822638, 0.957304 0.842449, 1.038744 0.843864, 1.028756 0.859431, 1.049500 0.865091, 1.058719 0.876411, 1.077159 0.882072, 1.086378 0.889147, 1.077159 0.901883, 1.024914 0.904714, 1.017231 0.908605, 1.100208 0.913204, 1.107122 0.936553, 1.130171 0.937261, 1.116342 0.967447, 1.159370 0.969806, 1.205310 0.978301, 1.104817 0.983956, 1.101525 1.000000, 1.167820 |
- 104 points. 172.71.154.39 19:17, 22 November 2022 (UTC)
- I only count 69 distinct dots, although a handful look like they might be merged pairs. What's up with that? 172.70.210.48 04:54, 26 November 2022 (UTC)
- Can someone please check my work https://colab.research.google.com/drive/1c_7Qj3S1VXtL-AckfSfHCd4ofGYYDYH5 and tell me if I'm doing it right? I'm pretty sure I don't really know what I'm doing. I kind of cargo cult-coded the Savitzky-Golay filter stuff linked from the explanation and have zero understanding of what's actually going on. 172.70.211.126 21:58, 22 November 2022 (UTC)
- Here's how Randall seems to be suggesting to do it, based on the light gray figures: [superceded] -- Can someone please help fix the residuals on the second plot? 172.71.154.158 01:18, 23 November 2022 (UTC)
- I fixed the residuals and added an inset confidence interval comparisons for the two slopes, split by both their maximum difference and by the maximum sum of the r2 values: https://colab.research.google.com/drive/1apKDIN5FE32mtGiQew5cE6wK6m6eM_Fr It's not clear from the gray text which method Randall is suggesting. 172.70.211.126 22:07, 24 November 2022 (UTC)
- I added this to the end of the Colab notebook:
- I fixed the residuals and added an inset confidence interval comparisons for the two slopes, split by both their maximum difference and by the maximum sum of the r2 values: https://colab.research.google.com/drive/1apKDIN5FE32mtGiQew5cE6wK6m6eM_Fr It's not clear from the gray text which method Randall is suggesting. 172.70.211.126 22:07, 24 November 2022 (UTC)
- Here's how Randall seems to be suggesting to do it, based on the light gray figures: [superceded] -- Can someone please help fix the residuals on the second plot? 172.71.154.158 01:18, 23 November 2022 (UTC)
# Later in the Explainxkcd explanation, a "Significance of the Difference between Two Slopes Calculator" # at https://www.danielsoper.com/statcalc/calculator.aspx?id=103 is recommended, so ... we get: # split by maximum slope difference: (as shown in green and red) # t-Value: 5.52246856 # Degrees of freedom: 100 # Probability: 0.00000027 (significant as < 0.05) # split by maximum sum of r²s: # t-Value: 6.25478825 # Degrees of freedom: 100 # Probability: 0.00000001 (also very significant) # So, while the latter might technically be about 27 times more likely, both represent undoutably # different linear fits. Perhaps someone can ask Randall which he was suggesting, if indeed either?
- What's the most reliable way to ask Randall this? Twitter? Email? Google Chat? 172.71.158.91 23:08, 24 November 2022 (UTC)
- Why don't you generate a series of mildly noisy datasets of two slightly different but random lines each and see which method gets closest to the generating parameters? Also, please put more blank lines in your code, and consider right-aligning the comments. 172.70.211.146 01:56, 26 November 2022 (UTC)
- What's the most reliable way to ask Randall this? Twitter? Email? Google Chat? 172.71.158.91 23:08, 24 November 2022 (UTC)
What's funny is people are doing a lot of statistics and computer magic when you can just tilt your screen like the comic says and get the same effect :P 172.70.54.52 (talk) 16:14, 25 November 2022 (please sign your comments with ~~~~)
- (Ɔ┴∩) ᄅᄅ0ᄅ ɹǝqɯǝʌoN ϛᄅ 'ㄣϛ:ㄥƖ ᄅᄅᄅ˙ᄅ9Ɩ˙0ㄥ˙ᄅㄥƖ ¡ƃuoɹʍ ʇᴉq ɐ ʇuǝʍ ƃuᴉɥʇǝɯos ʇnq 'ʇɐɥʇ pǝᴉɹʇ I
