Difference between revisions of "1862: Particle Properties"
(→Explanation: typo) |
(→Explanation: fix link, explain more) |
||
| Line 95: | Line 95: | ||
| The term "entropy", which {{w|History of entropy|began}} as a {{w|Entropy (classical thermodynamics)|thermodynamic measure}}, has since been adopted {{w|Entropy in thermodynamics and information theory|by analogy}} into {{w|Entropy (disambiguation)|multiple seemingly unrelated domains}} including, for example, information theory. The table allows that the term "entropy" must mean something in the context of particle physics, but isn't certain whether it's the classical, Gibbs' modern {{w|Entropy (statistical thermodynamics)|statistical mechanics}}, Von Neumann's {{w|Von Neumann entropy|quantum entropy}}, or some other meaning. | | The term "entropy", which {{w|History of entropy|began}} as a {{w|Entropy (classical thermodynamics)|thermodynamic measure}}, has since been adopted {{w|Entropy in thermodynamics and information theory|by analogy}} into {{w|Entropy (disambiguation)|multiple seemingly unrelated domains}} including, for example, information theory. The table allows that the term "entropy" must mean something in the context of particle physics, but isn't certain whether it's the classical, Gibbs' modern {{w|Entropy (statistical thermodynamics)|statistical mechanics}}, Von Neumann's {{w|Von Neumann entropy|quantum entropy}}, or some other meaning. | ||
| − | Imagine two identical balloons filled with the same gas and heated from two opposite sides with identical heat sources, creating symmetric temperature gradients in both; because the distribution of temperatures is the same, the Gibbs statistical thermodynamic entropy 𝑆 of the gas molecule particles in each balloon will be the same. In contrast, if one balloon is heated from one side by a low-power heat source and another by a high-power heat source, the balloon next to the high-power heat source will have a steeper temperature gradient, increasing the number of accessible microstates, hence the Gibbs entropies 𝑆<sub>low power</sub> < 𝑆<sub>high power</sub>. Now consider electrons in two atoms excited by absorbing identical photons to a mixed state; if the mixed states have the same probabilities for different energy levels, their Von Neumann quantum entropy 𝑆 values will be the same. Conversely, if one atom has electrons excited to a {{w|Purity_(quantum_mechanics)|pure}} | + | Imagine two identical balloons filled with the same gas and heated from two opposite sides with identical heat sources, creating symmetric temperature gradients in both; because the distribution of temperatures is the same, the Gibbs statistical thermodynamic entropy 𝑆 of the gas molecule particles in each balloon will be the same. In contrast, if one balloon is heated from one side by a low-power heat source and another by a high-power heat source, the balloon next to the high-power heat source will have a steeper temperature gradient, increasing the number of accessible microstates, hence the Gibbs entropies 𝑆<sub>low power</sub> < 𝑆<sub>high power</sub>. Now consider electrons in two atoms excited by absorbing identical photons to a mixed state; if the mixed states have the same probabilities for different energy levels, their Von Neumann quantum entropy 𝑆 values will be the same. Conversely, if one atom has electrons excited to a {{w|Purity_(quantum_mechanics)|pure state}} and another to a mixed state by photons of different energies, the mixed state will have higher entropy due to greater uncertainty, i.e., 𝑆<sub>pure</sub> = 0 and 𝑆<sub>mixed</sub> = ln(2). |
| + | |||
| + | In classical thermodynamics, entropy is typically a macroscopic property describing the disorder or randomness of a system with many particles. However, in statistical mechanics and quantum mechanics, the concept of entropy can also be applied to single particles under certain conditions. If the particle's position is not precisely known and can be described by a probability distribution, this contributes to entropy. Similarly, if the particle's momentum is uncertain and described probabilistically, this also contributes to entropy. A single quantum particle in a pure state (e.g., an electron in a specific atomic orbital) has zero entropy. This is because there is no uncertainty about the state of the system. If the single particle's state is described by a density matrix representing a mixed state (a probabilistic mixture of several possible states), the Von Neumann entropy can quantify the degree of uncertainty or mixedness of the state. | ||
| + | |||
| + | |||
|} | |} | ||
Revision as of 01:13, 30 May 2024
| Particle Properties |
 Title text: Each particle also has a password which allows its properties to be changed, but the cosmic censorship hypothesis suggests we can never observe the password itself—only its secure hash. |
Explanation
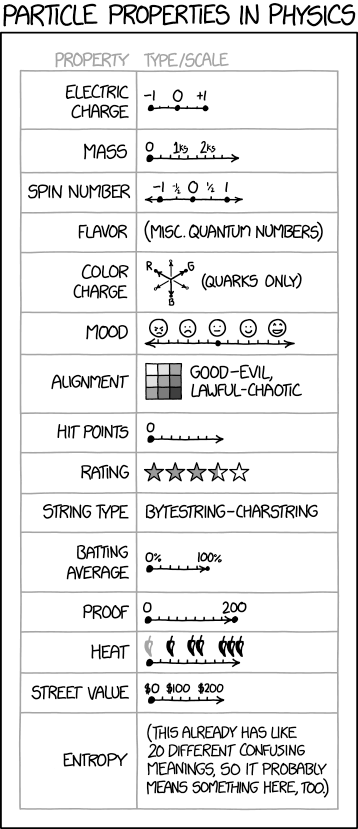
A table is presented comparing the range (maximum and minimum value) and scale (how big number increments are) of several measures. The table begins by listing properties pertinent to particle physics as the title suggests, but quickly devolves to other domains such as role-playing games (such as D&D) and sports after failing to provide a good definition of flavor.
| Property | Scale | Explanation |
|---|---|---|
| Electric charge | [-1,1] | The electric charge is shown in increments of a third from -1 to +1 which are the only known charges of fundamental particles (leptons, quarks and gauge bosons); however there are some exotic composite particles with twice integer charge, e.g. the recently discovered double charmed Xi baryon with a charge of +2.
Quarks are the only particles with charges of ± ⅓ or ± ⅔, but cannot exist individually; below the Hagedorn temperature, they are only found within hadrons. To date, all hadrons (particles composed of quarks), leptons, and bosons have integer charge, and current models indicate that this must be the case. |
| Mass | [0,∞) in kg | Mass (specifically rest mass) is the measure of an object or particle's resistance to force, as well as its ability to distort spacetime (its gravitational attraction).
Theoretically, any object's mass could approach infinity, but mass cannot be below 0 (as far as we know). The mass units shown (kilograms) are, however, far too large for particles. Some particles, such as photons, have zero rest mass and are therefore massless. All particles with rest mass obtain it through confinement, either by the Higgs field (the quarks; leptons; and W, Z, and Higgs bosons) or the strong nuclear force (hadrons). Particles with no rest mass (photons and gluons) can only move at lightspeed. |
| Spin number | (-∞,∞) (Intervals of ½) | Spin is an intrinsic property of particles, a relativistic form of angular momentum. The spin of a particle determines what statistics the particle follows, half odd integer spin particles are classified as fermions and integer spin particles are bosons.
Two fermions cannot have exactly the same state, an observation known as the Pauli exclusion principle. Thus, for fermions to exist in the same position, they must have opposite spins, of + ½ and - ½. It follows that a maximum of two fermions of the same flavor (e.g. two electrons) may exist in the same position. |
| Flavor | Misc. quantum numbers | Flavor is a series of quantum numbers that do not fit neatly onto a set of dimensional axes.
The most general theory breaks flavor down into four distinct conserved values, the electric charge, the weak isospin, the baryon number and the lepton number, but more specific models increase the number of distinct values. Quarks, for example, add five more flavor numbers: isospin (upness vs. downness), strangeness, charm, topness and bottomness (the last four are literally just the number of strange, charmed, top and bottom quarks, minus the corresponding anti-quarks). |
| Color charge | Coordinate system with R, G and B axes | The primary strong nuclear force has six mutually attractive charges, arranged in three perpendicular axes each analogous to electric charge. These charges are commonly referred to as "color" and the three axes are given the names of the three primary colors of light: Red, Green and Blue. The black dots in the diagram represent the actual colors while the white dots are the anti-color charges: anti-Red (colored cyan in diagrams), anti-Green (magenta) and anti-Blue (yellow). To complete the analogy, a color charge of zero is referred to as "White". The names of these charges are purely allegorical, but they do make it convenient to refer to them, especially in diagrams.
The color of a particle not confined by the strong force must be White, either as the sum of a color and its anti-color (as in a meson), as the sum of RGB or anti-RGB (as in a baryon), or as a sum of those sums (As in tetra-, penta- or hexaquarks). The attraction of the strong nuclear force is so strong that attempting to separate two quarks from each other creates enough energy to create two new quarks, which then bind to the original quarks. This property is known as "confinement" and means that color charge can never be observed directly. Randall is incorrect in stating "Quarks only", since gluons (the particle that carries the color force) are themselves colored. However, the colors of gluons are much more complicated, with a total of eight distinct superpositions of every possible color-anticolor pair. The fact that gluons are subject to the force they mediate also means that the strong force has a defined radius of effect, unlike the electromagnetic force, whose gauge bosons (the photon) are uncharged. This is the last entry currently used to describe particles by particle physicists. |
| Mood | 5 emojis on a number line ranging from angry to joyful | Particles are not considered to have mood, even in the allegorical way they have color or flavor, but Randall implies that there is a quantized 5 point scale (from "angry" to "ecstatic") which would have some effect on the properties of the particle. This would be more appropriate for measuring customer satisfaction. Charts such as this are also sometimes used in medicine to indicate levels of pain, and in some psychiatric treatments as a quick way to track changes in the patient's condition.
In grammar, particles are a nebulous class of words, usually defined by a lack of declension or conjugation (such as prepositions in English). Some languages use particles instead of or in addition to "standard" declension/conjugation, much like auxiliary verbs are used in English. These particles may well carry "mood" as an attribute, as well as tense and aspect. |
| Alignment | 3x3 grid with varying shades (columns Good-Evil, rows Lawful-Chaotic) | A reference to the tabletop RPG Dungeons & Dragons, where characters have an alignment that is either Good, Neutral, or Evil (describing whether they have a propensity to help or harm others) and either Lawful, Neutral, or Chaotic (describing how much they care about organizations, social norms, and the status quo). Common examples of these alignments include Darth Vader (Lawful Evil), Superman (Lawful Good), Robin Hood (Chaotic Good), and the Joker (Chaotic Evil). This may be a reference to the now defunct names of the two heaviest known quarks ("truth" and "beauty"). |
| Hit points | [0,∞) | Games (videogames, board games, CCGs, RPGs, etc.) often have values for players and other entities that represent health (also called hit points or HP). Generally there is not necessarily a limit on this value, but it does not often go below 0 as the zero value is considered "dead" (or some equivalent). |
| Rating | 5-star scale | The five-star rating system is often used to rate films, TV shows, restaurants, and hotels. Randall has previously criticized this system in 937: TornadoGuard and 1098: Star Ratings.
Interestingly, unlike the "Heat" rating with the chili peppers below, this scale doesn't have a creatively labeled number line, merely a rating (3.5, in this case). Considering 1098, could Randall be subtly self-deprecating here? |
| String type | Bytestring-Charstring | In computer science, this denotes what type of data is stored subsequent set of elements or a string. This is likely a pun on string types that appear in string theory and particle physics, and may also be a reference to Python, in which the difference between a byte string and a (Unicode) character string is a cause of difficulties for some programmers. |
| Batting average | [0,100] in % | In baseball, a player's batting average is calculated by dividing their hits by their at-bats. Instead of using the percent sign (%), it is usually presented as a number between 0 and 1 (inclusive) expressed as three decimal places with no leading zero: [.000, 1.000]. It is pronounced as though it is multiplied by 1,000: A batter with a batting average of .342 (which is very good) is said to be "batting three forty-two." A perfect batting average (unattainable except in very small samples) gives rise to the expression "batting a thousand." The 0-100 scale would be a better match for the batting average statistic in cricket, although percents would still not be used. |
| Proof | [0,200] | This refers to alcohol proof, which is the measure of the amount of ethanol in a beverage by volume. In the United States, 100 proof correspond to 50% alcohol, so the proof of a beverage is two times the percentage of ethanol, so the maximum value is 200. |
| Heat | No jalapeño icons - 3 jalapeño icons, increasing | Spicy dishes are sometimes measured by the intensity of the spicy flavor, usually ranging from values like "mild" to "hot". The gray jalapeño likely represents negligible or no spicy taste in the food. However, as an objective scale it is largely meaningless, since there is no reliable consistency in how these ratings are applied - what may be considered a 3-chilli dish in one establishment may only be a 1-chilli dish in another (as restaurants rarely if ever intend their dishes to be rated on the Scoville scale). The scale being unlimited may be a reference to the practice of some restaurants where a fourth or fifth chilli may be added to exaggerate the heat of their dishes. |
| Street value | [0,∞) in $ | The value of an illegal good or a legal/controlled good when bought or sold by illegal means usually by or to the end user. |
| Entropy | This already has like 20 different confusing meanings, so it probably means something here, too. | The term "entropy", which began as a thermodynamic measure, has since been adopted by analogy into multiple seemingly unrelated domains including, for example, information theory. The table allows that the term "entropy" must mean something in the context of particle physics, but isn't certain whether it's the classical, Gibbs' modern statistical mechanics, Von Neumann's quantum entropy, or some other meaning.
Imagine two identical balloons filled with the same gas and heated from two opposite sides with identical heat sources, creating symmetric temperature gradients in both; because the distribution of temperatures is the same, the Gibbs statistical thermodynamic entropy 𝑆 of the gas molecule particles in each balloon will be the same. In contrast, if one balloon is heated from one side by a low-power heat source and another by a high-power heat source, the balloon next to the high-power heat source will have a steeper temperature gradient, increasing the number of accessible microstates, hence the Gibbs entropies 𝑆low power < 𝑆high power. Now consider electrons in two atoms excited by absorbing identical photons to a mixed state; if the mixed states have the same probabilities for different energy levels, their Von Neumann quantum entropy 𝑆 values will be the same. Conversely, if one atom has electrons excited to a pure state and another to a mixed state by photons of different energies, the mixed state will have higher entropy due to greater uncertainty, i.e., 𝑆pure = 0 and 𝑆mixed = ln(2). In classical thermodynamics, entropy is typically a macroscopic property describing the disorder or randomness of a system with many particles. However, in statistical mechanics and quantum mechanics, the concept of entropy can also be applied to single particles under certain conditions. If the particle's position is not precisely known and can be described by a probability distribution, this contributes to entropy. Similarly, if the particle's momentum is uncertain and described probabilistically, this also contributes to entropy. A single quantum particle in a pure state (e.g., an electron in a specific atomic orbital) has zero entropy. This is because there is no uncertainty about the state of the system. If the single particle's state is described by a density matrix representing a mixed state (a probabilistic mixture of several possible states), the Von Neumann entropy can quantify the degree of uncertainty or mixedness of the state.
|
The title text says that in addition each particle has a password, but only hash of the password can be observed. This is a computer science reference. In computer science, properties (e.g. of an object or program) often can be changed with a single command. In physics as we observe it, properties can locally change with the environment. There are several experiments, whether physical constants are really time-const. Password hashing is the practice of hiding the password itself by storing only an irreversible representation of the password. Since the password itself is not stored, the password cannot ever be viewed by the user or a hacker (outside of the login page). This method is considered to be safest way of storing passwords. Password hashing using some key derivation function makes it impossible to steal passwords even if the server that stores hashes is cracked, unless the hash function is also broken, which should be a task which cannot be completed in any feasible time for sufficiently strong passwords. The title-text claims this is predicted by the cosmic censorship hypothesis, which in reality claims that a gravitational singularity must always be obscured by an event horizon (i.e.: there can't be a naked singularity). There is also a hint of quantum mechanics in the statement, as observation is one of the central concepts of the field, and Heisenberg's uncertainty principle actually states that it is impossible to observe (measure) some property of a particle with arbitrary precision when another one is known (e.g.: you can't determine the momentum and position of a particle). This makes the title text a mix of several domains, as was the above table.
Transcript
- Particle Properties in Physics
| Property | Type/scale |
|---|---|
| Electric charge | [Scale with -1, 0 and +1 labeled and markings dividing the units in thirds. The endpoints are both dots.] |
| Mass | [Scale with 0, 1kg and 2kg labeled and markings dividing the units into thirds. The endpoints are a dot on the zero end and an arrow on the other end.] |
| Spin number | [Scale with -1, -½, 0, ½ and 1 labeled and no additional markings. The endpoints are both arrows, pointing out.] |
| Flavor | (Misc. quantum numbers) |
| Color charge | [Coordinate system of three axes labeled R, G and B clockwise from the 10 o'clock position. Endpoints are arrow-dots on all ends, with black dots for the labeled ends and white dots for the unlabeled ends.] (Quarks only) |
| Mood | [Scale labeled with 5 emoticons, from angry to happy, and markings dividing the units in thirds. Endpoints are both arrows, pointing out.] |
| Alignment | [3x3 grid with varying shades] Good-Evil, Lawful-Chaotic |
| Hit points | [Scale starting from 0, markings but no labels other than zero. Endpoints are a dot at zero end and an arrow at the other end.] |
| Rating | [Star rating of 3.5/5 stars.] |
| String type | Bytestring-Charstring |
| Batting average | [Scale from 0% to 100%. Endpoints are dot at 0% end and arrow-dot at 100% end.] |
| Proof | [Scale from 0 to 200. Endpoints are dot at 0 end and arrow-dot at 200 end.] |
| Heat | [Scale labeled with pepper icons, from 0 (a grayed-out pepper) to 3 black peppers. Endpoints are a dot at zero end and an arrow at the other end.] |
| Street value | [Scale with $0, $100 and $200 labeled. Endpoints are a dot at zero end and an arrow at the other end.] |
| Entropy | (This already has like 20 different confusing meanings, so it probably means something here, too.) |
Discussion
oh dear, they copied the alt text wrong 173.245.50.108 14:58, 12 July 2017 (UTC)
More significantly, color charge is carried by gluons as well as quarks. Mjackson (talk) 15:19, 12 July 2017 (UTC)
As suggested by Zach Weinersmith ("For a joke: If you put pure alcohol under extreme pressure, could you claim to exceed 200 proof?"), it's kind of confusing that the comic suggests alcohol proof can exceed 200 proof, and also that baseball batting averages can exceed 100%. Although on further review, they use the arrow-dot →∙ notation rather than the dot-arrow ∙→, so maybe it's not intended to indicate a lack of an upper bound. But then I'm not sure what it does indicate, esp. compared to the Electric Charge property. Continuous vs. discrete? It doesn't seem clear… JohnHawkinson (talk) 15:41, 12 July 2017 (UTC)
- I think the arrow-dot is meant to mean "approaches, but does not (usually) reach" -- asymptotic behavior, in other words. 162.158.62.15 16:39, 14 July 2017 (UTC)
- Yes, I feel I can say with confidence that Arrow-Dot means "goes up to and including this number, but no more, this is the maximum", compared to the other scales with Dot-Arrow, which appear to mean "this dot/value is the highest you'll usually see, but it can be higher". For example the heat/spicy scale (I can't see it right now, can't remember what it's labelled as), the highest is 4 peppers and has a Dot-Arrow, but dishes which would be marked 4 Peppers would be relatively low on the Scovile Heat Scale (the actual scale for this). At one point I was looking into the heat scale, when I was figuring out the Frank's Red Hot sauces a local establishment carries, to see how much heat I like. The original Frank's lands at 450 Scovile Heat Units (SHU) and the Xtra Hot at 2,085 SHU. By comparison, Tabasco sauce is 2,500, the actual Tabasco pepper and Cayenne pepper are both between 30,000 to 50,000, Jalapeño averages 5,000 and the Ghost Chile Pepper over 800,000 and can top 1 million SHU. I'm sure the Tabasco, Cayenne and Ghost peppers are well above the scale in this comic. :) I read that the spiciest hot sauce you can buy commericially - as in without special mail order or something - is around 750,000 SHU. NiceGuy1 (talk) 04:36, 1 August 2017 (UTC)
Proof is presumably US proof - UK usage based on gunpowder 175 degrees proof would be 100% alcohol
Batting average is presumably from baseball Cricket batting averages are measured in runs per dismissal and are in theory unbounded. It is possible to have an infinite average for a season or series - though in terms of lifetime averages the best for players with more than ten matches is 99.96.
- If it is for baseball, it's labeled incorrectly. A perfect batting average is 1.000, not 100%. Batting average is actually a ratio - number of hits to number of at-bats - expressed as a decimal, not a percentage. For example, if a batter goes 3 for 5 in a game, his batting average would be .600, not 60%. OldCorps (talk) 16:25, 12 July 2017 (UTC)
We should probably arrange descriptions into a table.
How is it that there's no pain scale?
- Because Randall didn't think -- or possibly want -- to use it. Besides, do you really want every scale in existence in a single comic? If not, Randall has to select based on his own criteria, whatever they may be. As it is, there are 9 or 10 (depending on how you count "entropy") fields that don't apply to particle properties, as opposed to 5 or 6 that do. Gotta stop somewhere. Nyperold (talk) 22:44, 12 July 2017 (UTC)
- He could also have added the Volume scale, which would, of course, have been between 0 and 11.141.101.107.66 13:20, 13 July 2017 (UTC)
Actually, D&D calls you "dead" if you go to your NEGATIVE hit point maximum. Otherwise, you make a completely random (50%) death saving throw. After 3 cumulative fails, you die. After 3 cumulative successes, you are stable. More info can be found in the Player's Handbook. SilverMagpie (talk) 21:33, 12 July 2017 (UTC)
- According to the rules I know (Editions 3, 3.5 and Pathfinder) it's: 0 HP = unconscious; [-1; -CON) = dying (-> lose 1 HP each round unless you make a successful CON check); -CON = dead. http://www.d20pfsrd.com/gamemastering/conditions/#TOC-Dead Elektrizikekswerk (talk) 10:15, 13 July 2017 (UTC)
- In GURPS, your hit points can get even more negative. Below 0 hit points, you need to make a save each turn or fall unconscious; for each [HP] damage beyond that, you make a save against dying. At -5*[HP] hit points you die automatically; at -10*[HP] your body is more or less destroyed. (Also, in GURPS your hit points don't arbitrarily grow; an average character has between 5 and 15 hit points.) - Mike Rosoft (talk) 17:08, 15 July 2017 (UTC)
"Heat" measured in jalapeño has also been used by some email systems such as Eudora to measure how strong an email message is (e.g., whether it will lead to a flame war) 198.41.238.46 05:02, 13 July 2017 (UTC)
- Jalapeño measure between 2,500 to 8,000 Scoville Heat Units, or roughly 5,000 SHUs on average, so in theory you can assign objective values to a 1,2,3 jalapeño scale, i.e. 5000, 10000, 15000 SHUs RoyT (talk) 07:34, 14 July 2017 (UTC)
"String Type" being ByteString-CharString is a reference to Haskell, the programming language referenced in 1312: Haskell and used to make 1037: Umlaut, which is structurally obsessed with data types. ByteString is the go-to type for dynamic text, which in more literal form unpacks to a String of [Char]s. 108.162.246.65 08:41, 13 July 2017 (UTC)
The lower case g in Kg looks odd. I thought it was a strangely shaped 's'. WhiteDragon (talk) 20:35, 13 July 2017 (UTC)
Pretty sure the jalapeños are from ratemyprofessor.com: the tell is the grayed out one for zero 162.158.62.81 14:25, 14 July 2017 (UTC)
Marshall amps is unfortunately missing :-) : https://www.youtube.com/watch?v=4xgx4k83zzc 162.158.234.4
The table is quite similar to the tables in wolfram alpha. 162.158.178.221 11:16, 29 December 2021 (UTC)
Probably not even worth mentioning in the trivia, but liquor can never reach 200 proof. Distillation can't remove the last 10% or so of water from a water/ethanol solution, you have to dehydrate it chemically, e. g. by reacting it with a metal oxide to produce a hydroxide. Nitpicking (talk) 23:10, 10 April 2022 (UTC)