173: Movie Seating
| Movie Seating |
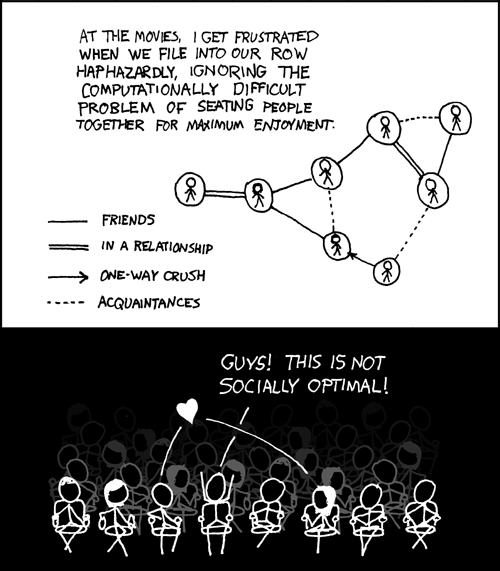 Title text: It's like the traveling salesman problem, but the endpoints are different and you can't ask your friends for help because they're sitting three seats down. |
Explanation[edit]
At the time of writing in most movie theaters in the US, seats were not reserved. That is, tickets were sold by screening without seat assignment, so an entering patron can take any vacant seat. Therefore, a group of incoming patrons may walk in a column and take a section of consecutive seats in a row, each person taking one next to the person in front of them. The order of these people is thus determined by the order in which they walk into the theater, which is in most cases random. After this comic was published, some theaters around the U.S. began to sell movie tickets with reserved seats, both online and when purchased at the theater. When you buy your ticket, you also specify which seat you would like to sit in. Therefore, if you buy multiple tickets, you can select seats that are adjacent to each other.
Cueball is upset at the way he and his friends have sat down at the movie theater. Part of the problem is that two people who are apparently in a relationship do not sit together. He therefore tries to use a social graph to calculate the best way for him and his seven friends to sit in a row, while taking into account all of the social connections among them. In mathematics, this type of problem is called combinatorial optimisation. The most popular example, the traveling salesman problem, is referenced in the title text, as well as in comics 287 and 399.
The title text shows that another part of the problem is that Cueball's friends, who could have helped him calculate a solution, are each sitting three seats away from him, and so he cannot ask them for help.
Solutions[edit]
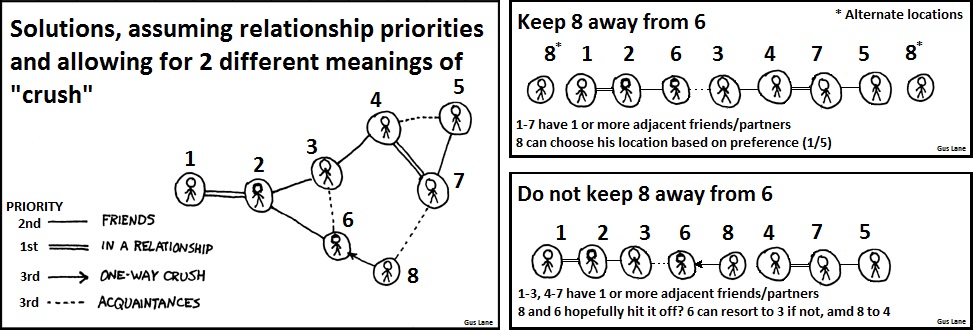
Solutions depend on how the "optimal seating" is defined: giving each connection type a "weight" and finding the highest possible sum value of achieved pairings, avoiding to have a "lonely" person without connections, or other goals are possible User:Squidy9002 wrote a program to find the best option through brute force, ignoring the one-way crush. According to their program, the best order is: 8, 5, 7, 4, 3, 6, 2, 1, although the function and pairing weights giving this as optimum are not known.
Two other hypothetical solutions for the specific problem proposed in the comic are here:
A solution that optimizes against "lonely" people and one-way crushes could have a seating of 1,2,6,3,4,5,7,8. This way, 1-7 have at least one friend or partner next to them, and 8 (who doesn't have friends or a partner in this group) has an acquaintance.
Transcript[edit]
- At the movies, I get frustrated when we file into our row haphazardly, ignoring the computationally difficulty problem of seating people together for maximum enjoyment.
- [Map of relationships between 8 people.]
- [Legend:]
- Single line: friends.
- Double line: in a relationship.
- Arrow: one-way crush.
- Dashed line: acquaintances
- [The eight friends sit in a row in a dark cinema. Cueball and one other are between two lovers.]
- Cueball: Guys! This is not socially optimal!
Trivia[edit]
In xkcd: volume 0, Randall says that this was his "passive-aggressive way of asking my friends to let me plan seating."
Discussion
I think that "two friends ... each sitting three seats away" takes "they" a little too literally. Daddy (talk) 06:17, 28 April 2013 (UTC)
Look at it like this. Placing them _friends_ apart guarantees lower background noise so you can actually watch the movie. 108.162.231.227 (talk) (please sign your comments with ~~~~)
Truthfully, I feel one-way crush should be second priority 05:09, 14 November 2015 (UTC) Lonely...
I know I'm horrifically late on this one, but surely swapping 4 and 7 is the solution which minimizes strangers in "Do not keep 8 away from 6". There is currently no path from 8 to 4. Swapping 4 and 7 downgrades the link to 5 to an Acquaintance from Friendship, but offers a viable path between all members. Unless we're intentionally forcing 8 to talk to 6? 162.158.99.64 08:20, 15 December 2015 (UTC)
The solutions are making assumptions about the weighting of friends, relationships, and acquaintances. For example, maybe someone in a relationship would achieve maximum enjoyment if the SO is seated next to a stranger so all focus is on them. -- Flewk (talk) (please sign your comments with ~~~~)
If we take the "keep 8 away" solution and put 8 in middle of 6 and 3, wouldn't the result be strictly superior to the "do not keep 8 away" one? It'd have the same number of adjacent relationships, but 6 would be seated next to a friend instead of an aquaintance, which is better. 141.101.104.82 16:38, 23 May 2016 (UTC)
8 doesn't know 1 or 5, so "keep 8 away" solution is bad. He would be alone then. 162.158.238.58 15:44, 24 December 2016 (UTC)
Maybe it's best to separate the couples so that no one has to be the third wheel. I propose [1,3,4,5,7,8,6,2]. Now, it might be unfair to #1, since his only connection is his girlfriend, so [3,4,5,7,8,6,2,1] works as well. 198.41.226.124 19:52, 15 August 2017 (UTC)
Bit of a naive solution, here. But if we assume the acquaintance is the weakest/least important of the relationships, we can just flatten the graph as if they were not there. So 8,6,1,2,3,4,7,5 (or 8,6,2,1,3,4,7,5 depending on who 1 would like to sit with more: 3 or 6) 172.68.34.172 20:11, 4 January 2020 (UTC)
- surely if you are trying to maximise enjoyment, and asuming a one way crush is equivalent to either a friend or an acquaintance for number 6, and a relationship for number 8, a more realistic option is [1,2,6,8,3,4,7,5] 172.68.210.47 07:01, 12 July 2022 (UTC)
In most movie theaters here in Atlanta, seats are indeed reserved. To deal with the declining profit margins and way that seating for anything but new blockbusters tends to be half empty, the theaters have replaced the small, uncomfortable festival seating with a small number of assigned recliners. I kid you not. It makes the high ticket prices seem more worthwhile. — Kazvorpal (talk) 04:16, 6 October 2019 (UTC)
I wrote a program to find the best option through brute force (ignoring the one-way crush). It's [8,5,7,4,3,6,2,1]
- Thx, i added it to the explanation --FaviFake (talk) 09:16, 22 March 2025 (UTC)
 Add comment
Add comment