2048: Curve-Fitting
| Curve-Fitting |
 Title text: Cauchy-Lorentz: "Something alarmingly mathematical is happening, and you should probably pause to Google my name and check what field I originally worked in." |
Explanation
| |
This explanation may be incomplete or incorrect: Please edit the explanation below and only mention here why it isn't complete. Do NOT delete this tag too soon. If you can address this issue, please edit the page! Thanks. |
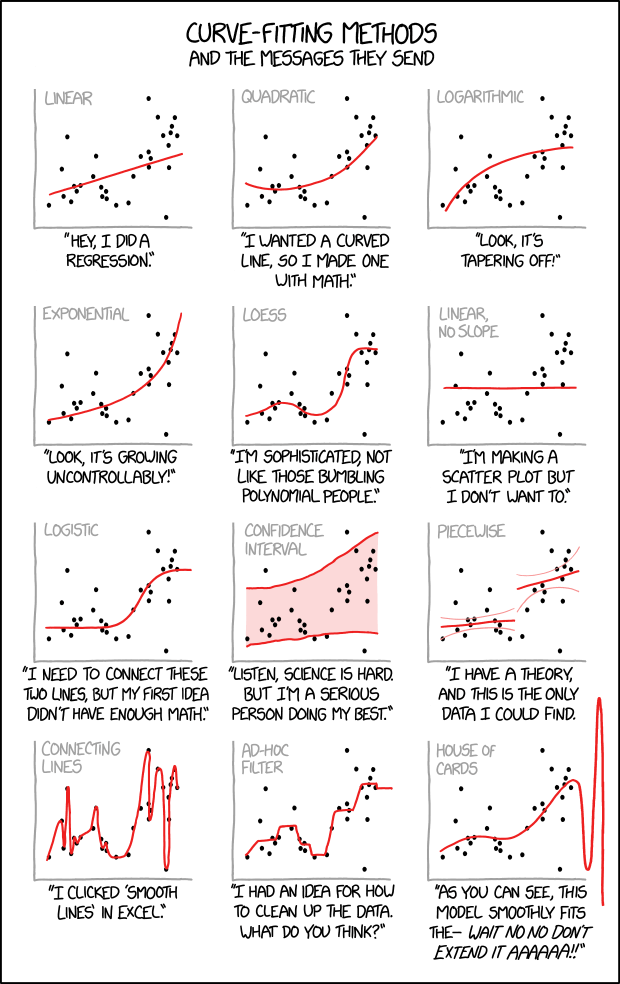
An illustration of several plots of the same data with curves fitted to the points, paired with conclusions that you might draw about the person who made them.
When modeling a phenomenon statistically, it is common to search for trends, and fitted curves can help reveal these trends. Much of the work of a data scientist or statistician is knowing which fitting method to use for the data in question. Here we see various hypothetical scientists or statisticians each applying their own interpretations, and the comic mocks each of them for their various personal biases or other assorted excuses.
In general, the researcher will specify the form of an equation for the line to be drawn, and an algorithm will produce the actual line.
This comic is similar to 977: Map Projections which also uses a scientific method not commonly thought about by the general public to determine specific characteristics of one's personality and approach to science.
Regressions have been the subject of several previous comics. 1725: Linear Regression was about linear regressions on uncorrelated or poorly correlated data. 1007: Sustainable and 1204: Detail depict linear regressions on data that was actually logistic, leading to bizarre extrapolations. 605: Extrapolating shows a line extrapolating from just two data points.
Linear
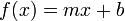
Linear regression is the most basic form of regression; it tries to find the straight line that best approximates the data.
As it's the simplest, most widely taught form of regression, and in general derivable function are locally well approximated by a straight line, it's usually the first and most trivial attempt of fit.
Quadratic
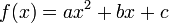
Quadratic fit (i.e. fitting a parabola through the data) is the lowest grade polynomial that can be used to fit data through a curved line; if the data exhibits clearly "curved" behavior (or if the experimenter feels that its growth should be more than linear), a parabola is often the first stab at fitting the data.
Logarithmic
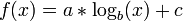
A logarithmic curve is typical of a phenomenon whose growth gets slower and slower as time passes (indeed, its derivative - i.e. its growth rate - is 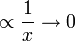 for
for 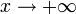 ), but still grows without bound rather than approaching a horizontal asymptote. (If it did approach a horizontal asymptote, then one of the other models subtracted from a constant would probably be better, e.g.
), but still grows without bound rather than approaching a horizontal asymptote. (If it did approach a horizontal asymptote, then one of the other models subtracted from a constant would probably be better, e.g. 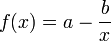 or
or 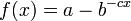 .) If the experimenter wants to find confirmation of this fact, they may try to fit a logarithmic curve.
.) If the experimenter wants to find confirmation of this fact, they may try to fit a logarithmic curve.
Exponential
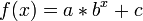
An exponential curve, on the contrary, is typical of a phenomenon whose growth gets rapidly faster and faster - a common case is a process that generates stuff that contributes to the process itself, think bacteria growth or compound interest.
- The logarithmic and exponential interpretations could very easily be fudged or engineered by a researcher with an agenda (such as by taking a misleading subset or even outright lying about the regression), which the comic mocks by juxtaposing them side-by-side on the same set of data.
LOESS
 (notice: this is just the function used for the weights, not the actually fitted curve formula, as it's a piecewise polynomial)
(notice: this is just the function used for the weights, not the actually fitted curve formula, as it's a piecewise polynomial) A LOESS fit doesn't use a single formula to fit all the data, but approximates data points locally using different polynomials for each "zone" (weighting differently data points as they get further from it) and patching them together
As it has much more degrees of freedom compared to a single polynomial, it generally "fits better" to any data set, although it is generally impossible to derive any strong, "clean" mathematical correlation from it - it is just a nice smooth line that approximates well the data points, with a good degree of rejection from outliers.
Linear, No Slope
Apparently, the person making this line figured out pretty early on that their data analysis was turning into a scatter plot, and wanted to escape their personal stigma of scatter plots by drawing an obviously false regression line on top of it. Alternatively, they were hoping the data would be flat, and are trying to pretend that there's no real trend to the data by drawing a horizontal trend line.
Logistic
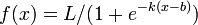
A logistic curve provides a smooth, S-shaped transition curve between two flat intervals; indeed the caption says that the experimenter just wants to find a mathematically-respectable way to link two flat lines.
Confidence Interval
Not a type of curve fitting, but a method of depicting the predictive power of a curve.Providing a confidence interval over the graph shows the uncertainty of the acquired data, thus acknowledging the uncertain results of the experiment, and showing the will not to "cheat" with "easy" regression curves.
Piecewise
Mapping different curves to different segments of the data. This is a legitimate strategy, but the different segments should be meaningful, such as if they were pulled from different populations.
This kind of fit would arise naturally in a study based on a regression discontinuity design. For instance, if students who score below a certain cutoff must take remedial classes, the line for outcomes of those below the cutoff would reasonably be separate from the one for outcomes above the cutoff; the distance between the end of the two lines could be considered the effect of the treatment, under certain assumptions. This kind of study design is used to investigate causal theories, where mere correlation in observational data is not enough to prove anything. Thus, the associated text would be appropriate; �there is a theory, and data that might prove the theory is hard to find.
Connecting lines
Not useful whatsoever, but it looks nice! It can be caused by overfitting to the data set or not using curve-fitting tools correctly.
Ad-Hoc Filter
Drawing a bunch of different lines by hand, keeping in only the data points perceived as "good". Also not useful.
House of Cards
Not a real method, but a common consequence of mis-application of statistical methods: a curve can be generated that fits the data extremely well, but immediately becomes absurd as soon as one glances outside the training data sample range, and your analysis comes crashing down "like a house of cards". This is a type of overfitting.
Cauchy-Lorentz
Cauchy-Lorentz is a continuous probability distribution which does not have an expected value or a defined variance. This means that the law of large numbers does not hold and that estimating e.g. the sample mean will diverge (be all over the place) the more data points you have. Hence very troublesome (mathematically alarming).
Since so many different models can fit this data set at first glance, Randall may be making a point about how if a data set is sufficiently messy, you can read any trend you want into it, and the trend that is chosen may say more about the researcher than about the data. This is a similar sentiment to 1725: Linear Regression, which also pokes fun at dubious trend lines on scatterplots.
Transcript
| |
This transcript is incomplete. Please help editing it! Thanks. |
- Curve-Fitting Methods
- and the messages they send
- [In a single frame twelve scatter plots with unlabeled x- and y-axes are shown. Each plot consists of the same data-set of approximately thirty points located all over the plot but slightly more distributed around the diagonal. Every plot shows in red a different fitting method which is labeled on top in gray.]
- [The first plot shows a line starting at the left bottom above the x-axis rising towards the points to the right.]
- Linear
- "Hey, I did a regression."
- [The second plot shows a curve falling slightly down and then rising up to the right.]
- Quadratic
- "I wanted a curved line, so I made one with Math."
- [At the third plot the curve starts near the left bottom and increases more and more less to the right.]
- Logarithmic
- "Look, it's tapering off!"
- [The fourth plot shows a curve starting near the left bottom and increases more and more steeper to the right.]
- Exponential
- "Look, it's growing uncontrollably!"
- [The fifth plot uses a fitting to match many points. It starts at the left bottom, increases, then decreases, then rapidly increasing again, and finally reaching a plateau.]
- LOESS
- "I'm sophisticated, not like those bumbling polynomial people."
- [The sixth plot simply shows a line above but parallel to the x-axis.]
- Linear, no slope
- "I'm making a scatter plot but I don't want to."
- [At plot #7 starts at a plateau above the x-axis, then increases, and finally reaches a higher plateau.]
- Logistic
- "I need to connect these two lines, but my first idea didn't have enough Math."
- [Plot #8 shows two red lines embedding most points and the area between is painted as a red shadow.]
- Confidence interval
- "Listen, science is hard. But I'm a serious person doing my best."
- [Plot #9 shows two not connected lines, one at the lower left half, and one higher at the right. Both have smaller curved lines in light red above and below.]
- Piecewise
- "I have a theory, and this is the only data I could find."
- [The plot at the left bottom shows a line connecting all points from left to right, resulting in a curve going many times up and down.]
- Connecting lines
- "I clicked 'Smooth Lines' in Excel."
- [The next to last plot shows a echelon form, connecting a few real and some imaginary points.]
- Ad-Hoc filter
- "I had an idea for how to clean up the data. What do you think?"
- [The last plot shows a wave with increasing peak values.]
- House of Cards
- "As you can see, this model smoothly fits the- wait no no don't extend it AAAAAA!!"
Discussion
House of Cards: Not a real method, but a common consequence of mis-application of statistical methods: a curve can be generated that fits the data extremely well, but immediately becomes absurd as soon as one glances outside the training data sample range, and your analysis comes crashing down "like a house of cards". This is a type of _overfitting_
I'm pretty sure it refers to the TV show house of cards, the dots representing the quality of the series increasing until Netflix renewed it a bit too much 172.68.26.65 (talk) (please sign your comments with ~~~~)
- This was my initial interpretation as well, since you can hypothetically extend a literal house of cards indefinitely.172.68.58.83 14:23, 20 September 2018 (UTC)
Could someone familiar with the show expand on this? Also a potential reference to the TV show, House of Cards ("WAIT NO, NO, DON'T EXTEND IT!"). Some context on what that line meant in House of Cards would be helpful. - CRGreathouse (talk) 14:20, 21 September 2018 (UTC)
I'm a little mystified by the alt-text. Cauchy and Lorentz both seem like mathematically capable people. What am I missing? 172.69.62.226 17:46, 19 September 2018 (UTC)
- Google-Fu reveals that it's a continuous probability distribution. This isn't bad per se, but it is quite visually distinctive and also can be quite...concerning if the data set isn't one where probability should be an issue. Werhdnt (talk) 18:00, 19 September 2018 (UTC)
- This is not the issue, but the fact that the moments (such as mean and variance) of the distribution don't exist = converge. See edited explanation. So if you wanted to estimate the parameters of the distribution, taking the sample mean for example will not converge with the number of data points, and is therefore bad to attempt. It is more mathematically alarming than alarmingly mathematical. GamesAndMath
- My own Google-Fu brought me to a page with this information: “The distribution is important in physics as it is the solution to the differential equation describing forced resonance, while in spectroscopy it is the description of the line shape of spectral lines.” (from here: https://www.boost.org/doc/libs/1_53_0/libs/math/doc/sf_and_dist/html/math_toolkit/dist/dist_ref/dists/cauchy_dist.html) Justinjustin7 (talk) 18:09, 19 September 2018 (UTC)
- True, but the "check what field I originally worked in" indicates that there might be something else going on with the meaning. 108.162.237.238 12:47, 20 September 2018 (UTC)
- I believe the point of "check what field I originally worked in" is that if somebody wasn't trained in statistics using an exotic distribution is highly suspect and suggest that either they are torturing the data to get desired results or have no idea what they are doing. 108.162.246.11 05:19, 21 September 2018 (UTC)
To be honest, I'm a bit disappointed. I kinda expected a special comic with such a nice round number.. Been counting down since comic #2000... 162.158.92.184 18:14, 19 September 2018 (UTC)
Different anon here, I think this is very special and if Randall makes a poster available I will be buying several to give away. Of course, part of my business is experimental data analysis and modeling...and this is a fantastic summary of common errors. 162.158.75.22 (talk) (please sign your comments with ~~~~)
- Agreed. This is a very special comic, and a highly subtle title text. Direct any of your friends who do data analysis here. Sort of the next stage from the classic "correlation is not causation" comic https://xkcd.com/552/ . -- GamesAndMath (talk) (please sign your comments with ~~~~)
Curve-Fitting
How fitting works needs to be explained. f(x)=mx+b works fine for single values, but how do we get that red line from the data set? --Dgbrt (talk) 20:12, 19 September 2018 (UTC)
- Generally, you decide for some error function and then search for parameters where the sum of errors for all data points is minimal. -- Hkmaly (talk) 22:07, 19 September 2018 (UTC)
- A typical error function is the square of the difference between the fit and the actual data point, hence "sum of squares" method. There are well-known standard formulas for finding m and b in the case of linear regression. In a linear algebra class, I saw a general method that would work for several of these (any where the fit is y = af(x)+bg(x)+...+ch(x), which includes log, exponential, quadratic, cubic, etc). I wish I could remember it. Blaisepascal (talk) 22:39, 19 September 2018 (UTC)
- I wish we could include the graphics at the top of [1] and [2] in the explanation. A lot of people are going to look at this one. 172.68.133.168 17:51, 20 September 2018 (UTC)
The data points do not have error bars, which makes the choice of fit even more ludicrous, in my opinion. If the data are that good, then I don't believe there is a correlation, it's random with some distribution. I might hang this up at work...Arppix (talk) 02:46, 20 September 2018 (UTC)
- And of course in serious science data points have error bars. This makes the fitting even more complicated and should be mentioned at the explanation. Because Randall doesn't use error bars I'm sure he refers to presentations not based on real science. Also this should be mentioned here. --Dgbrt (talk) 21:06, 20 September 2018 (UTC)
I hate to be negative here, as obviously some users have put a lot of effort into explaining the details behind each of the curve-fitting methods, but there's absolutely no explanation for Randall's comments on each method. While someone might learn something about the various methods by reading the explanation, they would not gain any insight on what Randall is saying about each method. In addition, the Connecting Lines explanation totally missed the fact that this isn't really even a curve-fitting method - it's just a feature of graphing software (in this case, Excel) where a smooth line is drawn through each data point from left to right rather than an example of overfitting to the data set. I think we could do better. Ianrbibtitlht (talk) 02:53, 21 September 2018 (UTC)
- You're not negative, Randall's comments are missing which I've just added into the incomplete reason. And sure other explanations still need a review. --Dgbrt (talk) 20:32, 21 September 2018 (UTC)
Everyone is missing the deeper trolling here of the fisheries community at large, which shall become blindingly clear here. First, this is cartoon number 2048 (2^11), a highly interesting number. Notably, this is the year all fisheries were projected to be collapsed by Worm et al. (2006) Science 314:787-790, a prediction which gained huge attention in the media and took on a life of its own. The prediction was based on fitting a power curve to some data on collapses in catch trends. Numerous rebuttals followed, one of which pointed out that a linear fit to the data is a better fit, and predicts all fisheries collapsed in 2114 (Jaenike et al. 2007, Science 316:1285a). A list of rebuttals is found here: https://sites.google.com/a/uw.edu/most-cited-fisheries/controversies/2048-projection. Later work by the same author and critics found a different prediction and showed rebuilding of fisheries is likely (Worm et al. 2009 Science 325:578-585). Second, lest you think this is a conspiracy theory, I note that in xkcd cartoon 887, Munroe specifically notes this prediction "The future according to google search results... 2048: "Salt-water fish extinct from overfishing" https://xkcd.com/887/. Third, this kind of model-fitting exercise has long plagued fisheries researchers attempting to predict recruitment from spawning biomass. 108.162.246.11 (talk) (please sign your comments with ~~~~)
"Ad hoc filter: Drawing a bunch of different lines by hand, keeping in only the data points perceived as "good". Also not useful. " – I guess it rather refers to data filtering, where for each point you take several points around and try to calculate some kind of mean, e.g. by rejecting most extreme points, or calculating median (see https://en.wikipedia.org/wiki/Median_filter). So it is an algorithm, not actually drawing lines by hand. Still it is tricky to draw conclusions and you can easily fool yourself with this method. 162.158.93.21 (talk) (please sign your comments with ~~~~)
Anyways, what is the actual regression of the plot? 162.158.154.241 (talk) (please sign your comments with ~~~~)
- This also must be better explained: We don't know what the points represent. The fraction of apples vs. bananas harvested by time, the position of stars in the sky, on a logarithmic scale, linear, or maybe the height of mountains in New Jersey... There are just some dots on paper with no further meaning. Thus everything Randall presents is valid by some means but an actual regression does not exist. --Dgbrt (talk) 20:32, 21 September 2018 (UTC)
Just want to note that the Piecewise models is actually a type of modelling often used in housing economics. It has been used to check if different types of housing are priced according to different rules. 172.68.34.34 22:05, 21 September 2018 (UTC)
Excel's "smooth lines" are actually splines (third-order Bezier splines, apparently) so they're not completely without mathematical merit. Still wildly unsuited for extrapolation, but often very well suited to interpolation. JohnWhoIsNotABot (talk) 21:44, 24 September 2018 (UTC)
Specific functions
In both the logarithmic and exponential functions, I have deleted the term "+ c" that was present in both. Simply put, these functions do not include an additive constant. To include the constant removes a basic property of e.g. exponential functions, which is that the function should grow by the same factor for equal increases in the value of x. (In other words, if the functions doubles when x changes from 1 to 2, then it should double again when x changes from 2 to 3, or from 3 to 4, etc.) If this does not happen, the function is not exponential. Redbelly98 (talk) 19:52, 13 October 2018 (UTC)
Logistic Curve
The explanation for logistic curve currently says it is used for binary values. It's actually a lot more useful than that. For example, population growth is often described as a logistic curve. It appears to be climbing exponentially initially, but then tapers off as resources can no longer support the population. 108.162.246.191 15:31, 8 November 2018 (UTC)
- The explanation mentions the logistic regression ranging between "0" and "1". It uses the more general logistic function you probably refer to. The logistic regression uses in its basic form a logistic function to model a binary dependent variable. Both Wikipedia links explain the difference. Honestly, I'm not an expert on that matter but that binary interpretation wouldn't allow values above "1" or below "0" as shown in the picture. Maybe worth to be mentioned. Nonetheless all other fittings are also similar nonsense. Maybe we could mention the more general Sigmoid function but this only barely fits to the title "Logistic Curve". --Dgbrt (talk) 23:09, 8 November 2018 (UTC)
Personally, I think the exponential fit seems like the most reasonable interpretation of the data.
Is the bottom right one considered as part of the Runge Phenomenon?"
As learnt in college, where trying to build an overlapping polynomial equation to a graph would create a working model until you move to the side and see the equation that worked until now going way off base 19:56, 3 April 2023 (UTC)D
