2117: Differentiation and Integration
Explanation
| |
This explanation may be incomplete or incorrect: Created by a BESSEL FUNCTION? Please mention here why this explanation isn't complete. Do NOT delete this tag too soon. If you can address this issue, please edit the page! Thanks. |
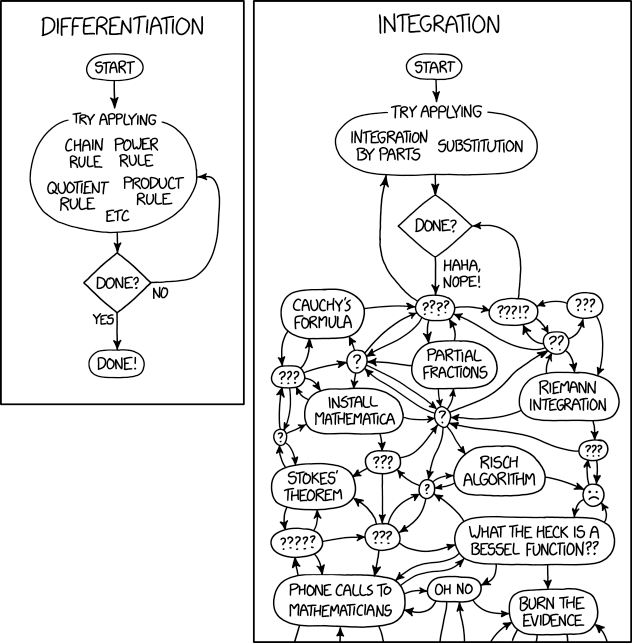
This comic provides a flowchart purporting to show the process of differentiation, and another for integration.
Differentiation and Integration are two major components of calculus. As many Calculus 2 students are painfully aware, integration is much more complicated than the differentiation it undoes.
However, Randall dramatically overstates this point here. After the first step of integration, Randall assumes that any integration can not be solved so simply, and then dives into a step named "????", suggesting that it is unknowable how to proceed. (The four ?s are not all on the same line, which implies further chaos and confusion.) The rest of the flowchart is (we can assume deliberately) even harder to follow, and does not reach a conclusion. This is in contrast to the simple, straightforward flowchart for differentiation.
It should be noted that Randall slightly undermines his point by providing four different methods, and an "etc", for attempting differentiation with no guidelines for selecting between them. (The "etc" in particular should not be here, as lists like this should name every single element without relying on the reader to be able to fill in unstated parts.)
Differentiation
For any 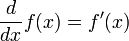 and
and 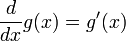 , it follows that
, it follows that 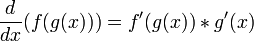 .
.
For any 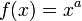 , it follows that
, it follows that 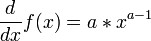 .
.
For any 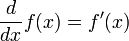 and
and 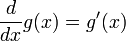 , it follows that
, it follows that 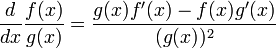 if
if 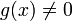 .
.
For any 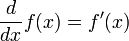 and
and 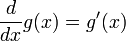 , it follows that
, it follows that 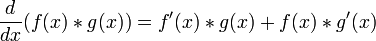 .
.
Integration
Substitution ???
Cauchy's Formula ???
Install Mathematica
Mathematica is a modern technical computing system spanning most areas. One of its features is to compute mathematical functions. This step in the flowchart is install and use Mathematica to compute to do the integration for you.
Stokes' Theorem ???
Risch Algorithm ???
Bessel Function ???
Symbolic integration Mentioned in the title text. ???
Transcript
| |
This transcript is incomplete. Please help editing it! Thanks. |
- [Two flow charts are shown.]
- [The first flow chart has four steps in simple order, one with multiple recommendations.]
- DIFFERENTIATION
- Start
- Try applying
- Chain Rule
- Power Rule
- Quotient Rule
- Product Rule
- Etc.
- Done?
- Yes
- No
- Done!
[The second flow chart begins like the first, then descends into chaos.]
- INTEGRATION
- Start
- Try applying
- Integration by Parts
- Substitution
- Done?
- Haha, Nope!
- [Chaos, Roughly from left to right, top to bottom, direction arrows not included.]
- Cauchy's Formula
- ????
- ???!?
- ???
- ???
- ?
- Partial Fractions
- ??
- ?
- Install Mathematica
- ?
- Riemann Integration
- Stokes' Theorem
- ???
- ?
- Risch Algorithm
- ???
- [Sad face.]
- ?????
- ???
- What the heck is a Bessel Function??
- Phone calls to mathematicians
- Oh No
- Burn the Evidence
Discussion
Darn, I have no idea what this comic is about. Randal has eluded my yet again. Linker (talk) 17:43, 27 February 2019 (UTC)
- Calculus. 162.158.79.143 18:16, 27 February 2019 (UTC)
And Calc 2 is why I stopped being a Computer Science major and moved (eventually) to majoring in English. Consistent 4.0s in math through Trig and Calc I ... 1.6 in Calc II, retook and got a 1.8. Without the Calc, couldn't do the physics; without the physics, couldn't get my 2-yr degree and move on from community college to a full university. I don't know what all the integration stuff in the flowchart is (since I didn't do well in Calc and it was a long time ago), but there's so very many things that become nonelementary integrals that all sorts of special tricks have to be employed for things that look like they should be easy. It's like having a problem that's very easy to do division on, but requires special advanced mathematical tricks to use multiplication upon.108.162.216.208 19:07, 27 February 2019 (UTC)
Going to start learning integration in 3 weeks... Wish me luck. 162.158.62.96 12:53, 3 November 2021 (UTC)
Basic ideas: Integration by parts is the reverse of the Product Rule. Substitution is the reverse of the Chain Rule. Cauchy's Formula gives the result of a contour integration in the complex plane, using "singularities" of the integrand. Partial fractions is just splitting up one complex fraction into a sum of simple fractions, which is relevant because they are easier to integrate. Stokes theorem is the relationship between an integral over an area, and an integral over the boundary of said area. Riemann integration was the first rigorous definition of integration. This has been superseded by Lesbesgue integration. Bessel functions are like 2d versions of sin and cos, and turn up sometimes when doing integration.162.158.89.61 20:14, 27 February 2019 (UTC)
- "Lesbesgue integration." Best. Freudian. Slip. Ever. SCNR :P 162.158.91.59 08:28, 28 February 2019 (UTC)
I know what you mean ;). After all, Gen 8 Pokemon was announced the other day, so you read it as "Pokemon League Integration". Completely understandable. 172.68.78.28 14:40, 28 February 2019 (UTC) Shouldn't Wolfram Alpha be somewhere in that flowchart? 162.158.255.142 20:54, 27 February 2019 (UTC)
Glad to see I'm not the only one who is too dumb to integrate 162.158.90.36 21:02, 27 February 2019 (UTC)
- Symbolic differentiation is just going through algorithm ; there are few functions which don't have it but they tend to be constructed in complicated way, and if function have differentiation it's usually easy to find it. Symbolic integration requires lot of thinking and trial and error ; even very easy function may lack primitive function and even if they don't, you may be unable to find it except randomly. If it's exercise in book, the ones for differentiation are done by thinking about some interesting function and putting it there. The ones for integration are done by thinking about some interesting function and putting it's differentiation there. -- Hkmaly (talk) 23:38, 27 February 2019 (UTC)
Oddly enough it mentions Riemann integration, but that is the integral most people know how to use. Turns out there are a lot more (e.g. lebesgue and generalized riemann integrals). I'm halfway through a second semester of real analysis and was floored by how involved integration can be. 172.68.34.106 21:36, 27 February 2019 (UTC)
One of my professors once said: "Never try to integrate a function. Almost all (in a strict mathematical sense) functions are impossible to integrate, so there is no reason why you should even try." --162.158.88.128 07:52, 28 February 2019 (UTC)
How is there no "+ C" joke in there Blagae (talk) 13:16, 28 February 2019 (UTC)
Probably because he put a +C joke in 1201:_Integration_by_Parts. 108.162.219.160 13:48, 2 March 2019 (UTC)
Why is all the maths broken GcGYSF(asterisk)P(vertical line)e (talk) 22:24, 4 May 2022 (UTC)
Risch algorithm
I thought I could contribute to the article with a better explanation of the Risch algorithm, since I have a bit of expertise here -- I've read all the original papers, plus the Cherry papers that add the extra features like Li and erf. I pulled out some of the old papers to review my knowledge of symbolic differential algebra (it's been a while!) then typed up a careful explanation which corrected some errors in the original description and fleshed out many more details... possibly excessively, but hey, that's kind of our calling here.
Then I saw that Glassvein completely removed my version for what appears to be the original without so much as a mention in the edit description. What gives? I
CRGreathouse (talk) 04:59, 28 February 2019 (UTC)
- Probably due to simultaneous editing. I've restored your definition. 162.158.88.128 16:52, 28 February 2019 (UTC)
- OK, wasn't sure if it was intentional (if somehow it was worse). Thanks! CRGreathouse (talk) 01:34, 1 March 2019 (UTC)
That was indeed an accident due to simultaneous editing. My bad! Glassvein (talk) 02:47, 5 March 2019 (UTC)
Numerical Integration
Better still...plot the graph - cut along the line - weigh the part under the line. :-) SteveBaker (talk) 20:46, 28 February 2019 (UTC)
[Anonymous: I understand mathematically that integration is much more difficult than differentiation, but is there a possibility that Randall is making the comment that the same is true for Society? Integration has proved very difficult, and has led to riots, but experience shows that dividing our society up into small subgroups (that then argue with each other, but don't spend enough time together for riots) is relatively easy.] 108.162.219.112 (talk) (please sign your comments with ~~~~)
- Good luck plotting Weierstrass function. -- Hkmaly (talk) 00:05, 9 March 2019 (UTC)
overstates the case?
Current summary says that the comic overstates the case of how difficult integration can be. I'm not sure that's true. Sure, you can use numerical integration to get a specific area under the curve, but that's not what the comic is referring to. Unless some mathematician can show here how integration can be done by repeatedly following a set of fixed rules, Ithis comic is actually completely accurate. And that's why it's funny. :-)
Purify the Power rule?
The derivative power rule shown is combined with the chain rule. I think it should be stated to be a pure power rule, without the chain rule components. When I tried making that adjustment, I got error messages that I could not resolve, so could someone who knows how the MATH feature works remove the chain rule from the power rule? Nutster (talk) 18:44, 26 December 2021 (UTC)