2533: Slope Hypothesis Testing
| Slope Hypothesis Testing |
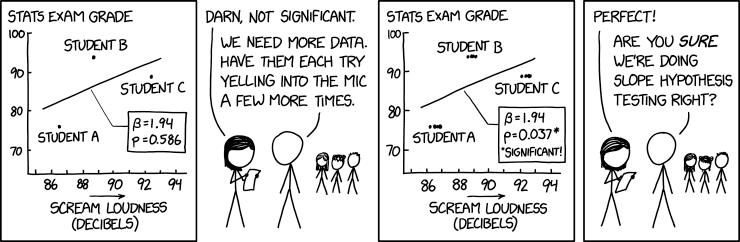 Title text: "What? I can't hear--" "What? I said, are you sure--" "CAN YOU PLEASE SPEAK--" |
Explanation
| |
This explanation may be incomplete or incorrect: Created by a SCREAMING STATISTICALLY SIGNIFICANT STATISTICS STUDENT. Note: there's a name for when the bone in your ear pulls away after exposure to loud noise, could be thematic to reference it. There's probably also a name for the statistical mistake the comic demonstrates. Do NOT delete this tag too soon. If you can address this issue, please edit the page! Thanks. |
"Slope hypothesis testing" is a method of testing the significance of a hypothesis involving a scatter plot.
In this comic, Cueball and Megan are performing a study comparing student exam grades to the volume of their screams. Student A has the worst grade and softest scream, but Student B has the best grades and Student C the loudest scream. A trendline has been plotted, indicating a positive correlation between grades and volume...but the p-value is extremely high, indicating little statistical significance to the trend. P-value is based on both how well the data fits the trendline and how many data points have been taken; the more data points and the better they fit, the lower the p-value and more significant the data.
Megan complains about the insignificance of their results, so Cueball suggests having each student scream into the microphone a few more times. This is incorrect, because it only provides more data on the screaming without providing more data on its relation to exam scores, and is a joke around poor statistical calculations likely made in the field today. The p-value is incorrectly recalculated based on the increased number of measurements. Each student has exactly the same test scores (probably referencing the same datum as before) and have vocal volume ranges that don't drift far either (each seems to have a range of scream that is fairly consistent and far from overlapping). Megan is pleased by these results, but Cueball belatedly realizes this technique may not be scientifically valid.
Measuring data multiple times can be a way to increase its accuracy, but does not increase the number of data points with regard to another metric, and the horizontally clustered points on the chart make this visually clear.
The common p-value formulae assume the data points are statistically independent, that is, that the test score and volume measurement from one point don't reveal anything about those of the other points. By reusing the same exam scores separately across several measurements each, Cueball and Megan violate the independence assumption and invalidate their significance calculation.
In current AI, there's a push toward "few short learning", where only a few data items are used to form conclusions, rather than the usual millions of them. This comic displays danger associated with using such approaches without understanding them in depth.
Additionally, a common theme in some research is the discovery of correlations that do not survive independent reproduction. This is because randomness with too few samples produces apparent correlations, and Randall has repeatedly made comics about this error of hope.
In the title text, Megan and Cueball are trying to yell over each other, asking each other to speak up so they can be heard, presumably because they are having trouble hearing from the yelling experiment.
Transcript
| |
This transcript is incomplete. Please help editing it! Thanks. |
Discussion
In the line "Randall has repeatedly made comics about this hopeful error", should specific examples be provided? I know /882 is one, but I'm blanking on any others. 172.68.132.114 10:21, 26 October 2021 (UTC)
- Definitely, otherwise it would not be very useful. --162.158.203.54 13:10, 26 October 2021 (UTC)
- hi, I added the line. <thinking-out-loud removed in copyediting>. I think there was one where article titles that blatantly used poor statistical techniques were listed, not sure. 172.70.114.3 14:40, 26 October 2021 (UTC)
I love it. Fwacer (talk) 02:52, 26 October 2021 (UTC)
I imagine that the problem here is that the errors are not independent. I can't find anything else wrong with this, but I feel like there's something obvious I'm not seeing. They might revoke my statistics degree if I miss something big here, hehe.--Troy0 (talk) 03:06, 26 October 2021 (UTC)
- The scores are clearly the one score they originally (sometime prior to the expanded test) received. Either that or multiple tests with the same exam questions without having given them enough feedback to change their answer-scheme at all. The volumes are probably a "good go at screaming" on demand, belying any obvious "test result -> thus intensity of scream" (what might be expected if the scream(s) of shock/joy/frustration were recorded immediately upon hearing a score).
- What they have here is a 1D distribution of scream-ability/tendency (which was originally a single datum), arbitrarily set against test scores. (Could as easily have been against shoe-size, father's income-before-tax, a single dice-roll, etc.)
- I initially assumed that the participants are screaming in response to learning their scores, so the relationship is not arbitrary -- the students with good scores sceam loudly with joy. Barmar (talk) 14:45, 26 October 2021 (UTC)
- Perhaps it was that (except the screaming volume is clearly confounded by other factors, such as how loudly they normally scream) but asking them to "scream again" seems to show far more personal correlation than emotional attachment, for they are the same people but time has passed to reduce the spontenity of the response and their newer submissions are at best "try to scream like you did when you heard your score the first time". Which is problematic and not really a valid new response to add to the list. At best, it's a test of replay consistency (now unlinked from the original feeling). 172.70.85.185 15:57, 26 October 2021 (UTC)
- I initially assumed that the participants are screaming in response to learning their scores, so the relationship is not arbitrary -- the students with good scores sceam loudly with joy. Barmar (talk) 14:45, 26 October 2021 (UTC)
- Whether there was an original theory that grades correlated with intensity of vocalisation is perhaps a valid speculation, but clearly the design of the test is wrong. Too few datum points, in the first instance, and the wrong way to increase them when they find out their original failing.
- The true solution is to recruit more subject. (And justify properly if it's intensity of spontaneous result-prompted evocations or merely general ability to be loud that is the quality the wish to measure. Either could be valid, but it's not obvious that the latter is indeed the one that they meant to measure.) 141.101.77.54 04:21, 26 October 2021 (UTC)
- It's pretty straightforward. This is a simple linear regression, Y = α + βX + ε, where α and β are parameters and ε is a random variable (the error term). Their point estimations for α and β are correct. But their confidence intervals (and thus p-values) are wrong, because they are based on a false assumption. They constructed their intervals assuming ε was normally distributed, which it clearly is not. ε will always be approximately normally distributed if the central limit theorem applies, but it does not apply here. The central limit theorem requires that the samples be independent and identically distributed. Here, they are identically distributed, but they are not remotely independent. After all, the same people were selected over and over again. Therefore ε will probably not be randomly distributed (it isn't even close), and the confidence intervals (and so p-values) are wrong. 172.70.178.47 09:10, 26 October 2021 (UTC)
- You seem to be the only person so far who's learned in academia why this is wrong. Is the current state of the article correct? 172.70.114.3 14:31, 26 October 2021 (UTC)
- The scientific error isn't quite what people are saying it is. The issue here is not "reusing a single test score" or an issue with non-normality of errors, the issue is that the data are *nested* within participants and that isn't being accounted for. There are fairly standard ways of managing this, at least in the social science literature (and these ways are statistically valid), most commonly the use of multilevel modeling (also known as hierarchical linear modeling). This accounts for the correlated nature of the errors. Now, even using the right method they're not going to attain statistical significance, but at least they aren't making a statistical mistake.
- You can look at it in different ways. Obviously the error they made in their research was sampling the same people repeatedly and assuming that could increase the significance of their result. But mathematically, the analysis fails because the errors are not normally distributed. The math doesn't care about how you gather data. If the random variables ε is normally distributed, you can calculate confidence intervals for the parameters and for predictions exactly. The sum of squared residuals will have a chi square distribution. In particular, this means the estimator for beta will be normally distributed, and therefore the standard error in the point estimator will have a (scaled and translated) t distribution. Knowing this, you can use the CDF for the t distribution to compute the p-value exactly. To explain what's wrong with this, we need to spot which assumption was in error. Here, the false assumption was the normality of ε. Even if ε is not normally distributed, as long as it has finite mean and variance, the mean of n independent samples will converge in distribution to z as n goes to infinity. But here, the samples are not independent. So even if you sampled these same kids infinitely many times, the distribution of errors will not converge to the normal distribution, so the assumption of normality remains false. (BTW, this is the same IP as before, just from my phone this time.) 172.70.134.131 19:40, 27 October 2021 (UTC)
I don't think the title text speakers are unidentified, I'm pretty sure it's a direct continuation of the dialogue in the last panel. Esogalt (talk) 04:11, 26 October 2021 (UTC)
- I agree. the second speaker starts to say "I said, are you sure--", this is the start of Cueball's last line. I think this is intended to be Cueball and Megan trying to talk about the results while the students are still screaming. TomW1605 (talk) 06:45, 26 October 2021 (UTC)
- It could also be the case that their hypothesis was true and they failed so badly at statistics, that their voices are inaudible now.
- Because, since they didn't write that test, their score is zero. 108.162.241.143 14:29, 26 October 2021 (UTC)
- It could also be the case that their hypothesis was true and they failed so badly at statistics, that their voices are inaudible now.
Is there a polynomial that better fits this data? 108.162.241.143 14:29, 26 October 2021 (UTC)
- Given three points, there's a circle that exactly fits them... ;) 172.70.85.185 15:57, 26 October 2021 (UTC)
- Also, infinite number of polynomials which fits this data exactly. -- Hkmaly (talk) 23:06, 26 October 2021 (UTC)
- But exactly one circle (assuming all mutually different, and not already upon a line), in an elegantly obvious manner. Therefore clearly the more individually significant statistical match for three datum points. :P 172.70.162.173 11:50, 27 October 2021 (UTC)
Speaking as the person who wrote the explanation for "slope hypothesis testing," we need someone to write a better explanation for it. It's just a placeholder meant to patch a gap until someone who knows what they're talking about (or what to google) can write a better one. GreatWyrmGold (talk) 14:30, 27 October 2021 (UTC)
- My (armchair) summary(!) would be that a general proposition is that there is a simple linear relationship between two factors (or their logs/powers/whatevers, reformulated as necessary) so those are plotted and their conformity to a gradient(±offset) is evaluated.
- The slope is defined by just two values which can, if necessary*, be emperically tested against the 'wrongness' of the points against the line (including error allowances) to find that line which is itself therefore minimally 'wrong', and that remaining wrongness (including how much of the possible error may need to be accepted) conveys the conformity or otherwise and you have also tied down the possibly unknown relationships - as best you are allowed to.
- * - though there are doubtless many different direct calculation/reformulation methods that don't require progressive iterations towards a better solution. And identify where multiple minima might lie in the numeric landscape.
- (Summary, indeed! This is why I didn't myself feel the need to try to do anything with the Explanation. It just seems like a typical Munrovian mash up of Statistical Hypothesis Testing and working with a slope. If I was ever taught this Slope-specific one (other than assessment by inspection, to preface or afterwards sanity-check loads of Sigma-based mathematics/etc that one can easily mess up by hand, or GIGO when plugged into a computer wrongly) then I've forgotten its name.) 172.70.91.50 15:19, 27 October 2021 (UTC)
What makes the graph even worse is that both axis don't start at zero.172.68.50.218
