2322: ISO Paper Size Golden Spiral
| ISO Paper Size Golden Spiral |
 Title text: The ISO 216 standard ratio is cos(45°), but American letter paper is 8.5x11 because it uses radians, and 8.5/11 = pi/4. |
Explanation[edit]
This is another comic on How to annoy people, here both graphic designers and mathematicians. This type of annoyance seems much like that displayed in 590: Papyrus and 1015: Kerning.
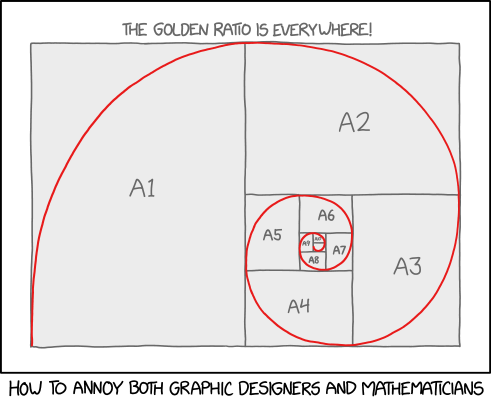
An easy way to annoy many mathematicians is to make fanciful claims about the Golden Ratio. It's been claimed, with varying levels of credibility, to be detectable in many natural and human-made situations, often with the dubious subjective claim that using the ratio in some particular way makes an image more "beautiful". The Golden Spiral is a spiral whose growth factor is this ratio; a common (though slightly geometrically inaccurate) way to illustrate the spiral is to draw curves through a set of squares whose side lengths shrink according to the Golden Ratio. The result looks rather like Randall's drawing here.
However, Randall hasn't used the Golden Ratio at all; he's just drawn a spiral (not the Golden Spiral) through a common diagram showing the A Series of standard paper sizes, but in landscape instead of portrait (this diagram is commonly drawn in portrait). These papers aren't squares at all, but rectangles whose side lengths shrink by a factor of the square root of 2. Additionally, the paper sizes shrink by a factor of one half, so the area is filled in a geometric series. This is sometimes called a silver rectangle, although the Silver ratio is actually 1+√2. By mistaking the A Series for something connected with the Golden Ratio, and perpetuating the tradition of making dubious claims about the Golden Ratio, Randall has successfully annoyed both graphic designers and mathematicians.
The title text is a similarly themed joke, based partly on the fact that the US uses customary units while the vast majority of the rest of the world uses SI units. The 11/8.5 ratio is the length/width ratio of US Letter paper, which is 11 inches by 8.5 inches (another common size in the United States is US Legal, which is 14" by 8.5"). The value of π/4 radians is indeed equal to 45 degrees, although Randall takes the cosine in one case and uses the raw angle in the other case in order to get a close coincidence of values. The width and length of A Series paper (ISO 216) is always given in whole millimeters, and the width/length ratio is very close to cos(45°) (which is 1/√2=0.707…) As for US Letter paper: to 4 decimal places, 8.5/11 = 0.7727 and π/4 = 0.7854.
In reality, the usage of radians vs. degrees is not a geographic or political decision, but generally is delineated by profession. Most engineering and science fields measure angles in degrees or fractions of degrees (arcseconds, or even milliarcseconds in fields like astronomy), while mathematicians and physicists generally use radians. Civil engineers may refer to the slope of a road by its grade, which is commonly expressed in terms of the tangent of the angle to the horizontal (either as a percentage or a ratio); for angles up to ~10°, this is close to the value of the angle in radians.
The difference between the "real" Golden Spiral squares and Randall's version is approximately either .2038 (for √2-1.6180…) or .08907 ((1/√2)-1.6180…), depending on which way you're counting. Either way, the difference would be very noticeable.
The spiral shown is approximately a logarithmic spiral with a growth factor of √2, although it has been edited slightly to make it fit neatly inside the rectangles. If the center of the spiral is at the origin, it may be graphed with r = C*2^(θ/π), for any positive constant C.
In 1488: Flowcharts a golden spiral has been laid in over the chart. That comic is a link that goes to the spiral page on xkcd.
Transcript[edit]
- [Caption inside panel:]
- The golden ratio is everywhere!
- [Picture of the ISO standard paper sizes (i.e. A1, A2, etc.) placed so that they fit together perfectly, overlaid with a spiral resembling that of the golden ratio]
- [A rectangle in landscape orientation with width= height*sqrt(2) is divided into two halves by a vertical line. The left half, a rectangle in portrait orientation, with height=width*sqrt(2), is labeled "A1". The right half (also portrait) is divided into two halves by a horizontal line; the rectangle above this horizontal line (landscape) is labeled "A2". Below this horizontal line there is a landscape rectangle which is divided into two portrait rectangles by a vertical line. The right half is labeled "A3", the left half is divided into two halves by a horizontal line. The lower half is labeled "A4", the upper half is divided again, with its left half labeled "A5". The series continues like this until "A10". ]
- [Symbolically: A1 -right,up- A2 -down,right- A3 -left,down- A4 -up,left- A5 -right,up- A6 -down,right- A7 -left,down- A8 -up,left- A9 -right,up- A10.]
- [A red spiral starts at the lower left corner of A1, passes through the upper right corner of A1 which is also the upper left corner of A2, continues through the upper right corner of A3, lower right of A4, lower left of A5, etc, and after passing through the lower right corner of A10 continues to what would be the lower left corner of A11 and the upper right corner of A12.]
- [Caption below panel:]
- How to annoy both graphic designers and mathematicians
Trivia[edit]
- The title text originally said 11/8.5 instead of 8.5/11. This has since been corrected.
Discussion
It annoys me that the hover text says 11/8.5 = pi/4, when 8.5/11≈0.77272727272 and pi/4≈0.78539816339. Claiming 8.5/11 equals pi/4 would be a much more beleiveable lie. 162.158.79.37 15:29, 19 June 2020 (UTC)
- The title text has since corrected this error!108.162.219.170 07:14, 25 June 2020 (UTC)
The explanation says that the A series "side lengths shrink by a factor of the square root of two" but that's not true. The width of A(n+1) is half the length of A(n) as depicted. The sqrt(2) ratio referenced is between the length and width of any one piece of paper.172.69.62.124 15:35, 19 June 2020 (UTC)
- The side lengths do shrink by a factor of sqrt(2): the width of A(n) is sqrt(2) times the width of A(n+1), the length of A(n) is sqrt(2) times the length of A(n+1). Your statement that "the width of A(n+1) is half the length of A(n)" is also true, but it does not contradict that each step in the A-series shrinks the sides by a factor of sqrt(2). Zmatt (talk) 16:09, 19 June 2020 (UTC)
Fixed it 162.158.74.61 15:43, 19 June 2020 (UTC)
Hi ! How come 11/8.5 = Pi/4 ? First one is more thant 1, second one is less than one... Although Pi/4 and 8.5/11 (or the reverse) are pretty similar, as usual in "let's annoy mathematicians" Randall's style...
I think y’all just got nerd sniped by Randall’s title text.
https://xkcd.com/spiral/ --188.114.103.233 17:22, 19 June 2020 (UTC)
I understand why it annoys mathematicians (it's not the golden ratio), but why does it annoy graphics designers? Please add explanation!
- I suspect that what would annoy many (if not most) graphic designers (especially Americans) is the claim that the ISO standard for paper sizes (which is very rarely used in the US) is inherently and objectively beautiful, along with the implication that everyone should switch to using the international standard.
- The usual graphic for this is vertical and has the paper sizes getting smaller going towards the top left corner, not positioned in a spiral.
- More scientifically-minded designers would be just as annoyed as (most) mathematicians are by the persistent myth that there is something inherently beautiful about the "golden ratio" in the first place, but unfortunately they are probably not in the majority.172.69.50.76 17:50, 21 June 2020 (UTC)
- I'm a graphic designer, and this doesn't annoy me. Perhaps because I'm not particularly fond of the golden ratio. I can only speak for myself. BleepBox (talk) 15:32, 30 June 2020 (UTC)
- Also a graphic designer. Doesn't annoy me either. Maybe if you're really obsessed with paper size standards, it might annoy you, but most graphic design work doesn't even follow ISO paper sizes, even outside the US (most of the time you're either working with whatever arbitrary size the printing house demands, or you're given the freedom to determine your own arbitrary size). 172.69.3.195 23:50, 23 March 2023 (UTC)
It should be noted that the logarithmic spiral this comic implies it is would actually go outside the bounds of the paper. The leftmost point of the spiral would be about 6.4mm to the left of the left edge of the A1 sheet. Zmatt (talk) 18:39, 19 June 2020 (UTC)
- This drawing (as opposed to the singular mathematical formula behind the idealised spiral for the partitioning used) basically takes a simple quarter-oval across each distinct sheet size (with, as essentially mentioned elsewhere, the root(2) ratio between sides) alternating x/y and y/x as major and minor axes respectively. Even if it is not obviously discontinuous (x and y inflection transitions occur subtly) any derivative of the curve (as polar, say) would show jumps in gradient at each stage - probably an inclined-stepped/saw-toothy pattern whereas the true logarithmic line would demonstrate itself as a continuous function at any such level of derivation. The true spiral line followed from origin outwards would almost (not quite, because of the polar gradient) hit the 'outer edge' first in line with the ultimately recursive centre-point then withdraw again to hit the next transition slightly 'inward' of the next level out. The Golden Spiral approximation uses squares for each quarter, which therefore does not switch major and minor axes, but still changes the curve and thus has the same not-quite-Golden nature. Although it's hard to describe, as you can see from my poor attempt that's probably inadvertently fallen foul of more specialised Pure Mathematics terminology due to the Pedant's Curse... ;) 162.158.155.240 22:23, 19 June 2020 (UTC)
Mathematicians get annoyed by the claim that the golden ratio is everywhere. I love Disney's "Donald in Mathmagic Land" but they make some outrageous claims about the golden ratio's place in art and architecture. BTW, the ISO system of paper sizes is awesome! You can photocopy two A4 pages side-by-side, reduced to fit exactly on a single A4 page.
- Also they get pi wrong. --162.158.79.209 22:18, 20 June 2020 (UTC)
- I think you mean that half of A4 is A3 ;o) 108.162.249.248 05:02, 24 June 2020 (UTC)
Isn't grade closer to degrees than to radians? Djbrasier (talk) 15:03, 20 June 2020 (UTC)
- It's two different things. The "grade" of a slope is just the rise divided by the run, commonly expressed as a precentage. It is not an angle measure but the tangent of an angle measure. It is commonly used in North America for surveying and engineering purposes. "Gradian" is a badly named angle measurement that, worse, is often referred to informally as "grade" from "centigrade".It is an angle measure, though a useless one: ten-ninths of the measure in degrees. The gradian is commonly used for surveying and engineering in some parts of Europe. The text in the current explanation confuses them, which is common due to the bad naming of the second measure. 162.158.187.197 16:45, 20 June 2020 (UTC)
A friend of mine, attempting to do graphic design, once created an approximate golden spiral using the boxes diagram with quarter circles. He then laboriously produced a logo by making copies of the spiral and using pieces of it for each curve. I then informed him that all the curves in his image were just circular segments. 172.69.69.44 16:36, 20 June 2020 (UTC)
108.162.216.216 15:21, 23 June 2020 (UTC)
The reason ISO paper sizes use an aspect ratio equal to the square root of two is that makes enlarging or reducing in copiers work better. With the US sizes, when you enlarge or reduce to the next standard size up or down, you have to choose between cutting off part of your original or leaving some blank space, because US standard paper sizes aren't the same shape.
It was done before photocopiers could do reduction or enlarging as cutting in half always produces the same shape of page.
108.162.216.216 15:21, 23 June 2020 (UTC)
- I never knew this, but it is no surprise. :P 108.162.249.248 05:03, 24 June 2020 (UTC)
 Add comment
Add comment
