Difference between revisions of "977: Map Projections"
(→Peirce Quincuncial: and the same comment as on my immediately previous edit) |
("No angle distortion" is also true of many projections in which a straight line does NOT have constant bearing, e.g. the stereographic projection. A non-mathematician must have contributed here.) |
||
| Line 14: | Line 14: | ||
===Mercator=== | ===Mercator=== | ||
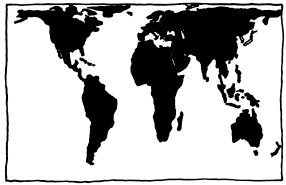
[[File:MercatorProjection.jpg|frame|The Mercator projection]] | [[File:MercatorProjection.jpg|frame|The Mercator projection]] | ||
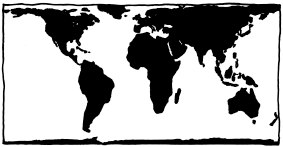
| − | The {{w|Mercator projection}} was introduced by Flemish cartographer Gerardus Mercator in 1569. The main purpose of this map is that at | + | The {{w|Mercator projection}} was introduced by Flemish cartographer Gerardus Mercator in 1569. The main purpose of this map is to preserve compass bearings; for example 13 degrees east of north will be 13 degrees clockwise from the ray pointing toward the top of the map, at every point. A mathematical consequence is the mapping is conformal, i.e. if two roads meet at a certain angle on the surface of the Earth, they will meet at that same angle on the map. It also follows that at every point the vertical and horizontal scales are the same, so locally i.e. considering only a small part of the map, geographical features (shapes, angles) are well represented, which helps a lot in recognizing them on-the-field, or for local navigation in that small part only. For this reason, that projection (or a close variant) is used in several online mapping services, such as Google Maps, which means that it is frequently encountered by the general public. A straight line on the map corresponds to a course of constant bearing (direction), which was very useful for nautical navigation in the past (and thus made that projection very well-known). |
However, from a global point of view, this projection is radically incorrect in how it shows the size of landmasses (for instance Antarctica or Greenland seem gigantic), and furthermore, it always excludes a small region around each pole (otherwise the map would be of infinite height), so it doesn't provide a complete solution for the problem of map projection. The comic implies that people who like that projection aren't very interested with map issues, and typically use what they are offered without thinking much about it. | However, from a global point of view, this projection is radically incorrect in how it shows the size of landmasses (for instance Antarctica or Greenland seem gigantic), and furthermore, it always excludes a small region around each pole (otherwise the map would be of infinite height), so it doesn't provide a complete solution for the problem of map projection. The comic implies that people who like that projection aren't very interested with map issues, and typically use what they are offered without thinking much about it. | ||
Revision as of 04:32, 24 November 2015
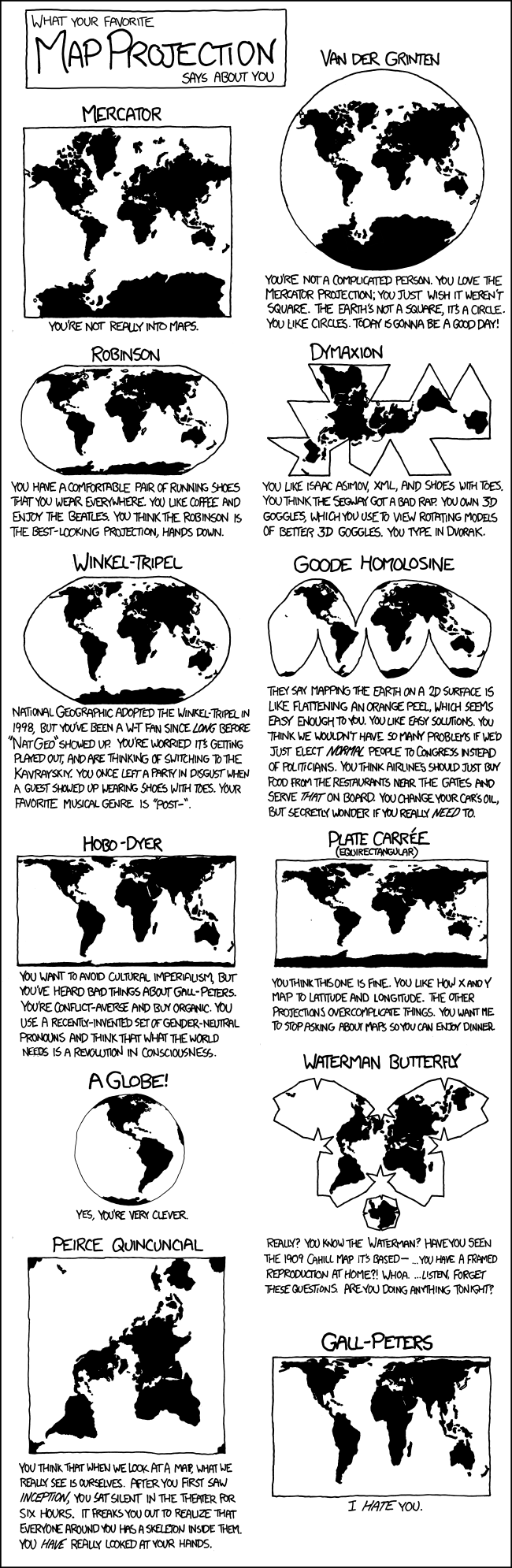
| Map Projections |
 Title text: What's that? You think I don't like the Peters map because I'm uncomfortable with having my cultural assumptions challenged? Are you sure you're not... ::puts on sunglasses:: ...projecting? |
Contents
Explanation
Map projection, or how to represent the spherical Earth surface onto a flat support (paper, screen...) to have a usable map, is a long-time issue with very practical aspects (navigation, geographical shapes and masses visualization, etc.) as well as very scientific/mathematical ones, involving geometry or even abstract algebra among other things. There is no universal solution to this problem: Any 2D map projection will always distort in a way the spherical reality. Many projections have been proposed in various contexts, each intending to minimize distortions for specific uses (for nautical navigation, for aerial navigation, for landmass size comparisons, etc.) but having drawbacks from other points of view. Some of them are more frequently used than others in mass media and therefore more well-known than others, some are purely historical and now deprecated, some are very obscure, etc.
Randall suggests here the idea that someone's "favorite" map projection can reveal aspects of their personality, then goes through a series of them to show what they can mean:
Mercator
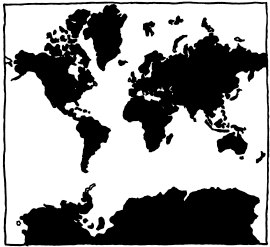
The Mercator projection was introduced by Flemish cartographer Gerardus Mercator in 1569. The main purpose of this map is to preserve compass bearings; for example 13 degrees east of north will be 13 degrees clockwise from the ray pointing toward the top of the map, at every point. A mathematical consequence is the mapping is conformal, i.e. if two roads meet at a certain angle on the surface of the Earth, they will meet at that same angle on the map. It also follows that at every point the vertical and horizontal scales are the same, so locally i.e. considering only a small part of the map, geographical features (shapes, angles) are well represented, which helps a lot in recognizing them on-the-field, or for local navigation in that small part only. For this reason, that projection (or a close variant) is used in several online mapping services, such as Google Maps, which means that it is frequently encountered by the general public. A straight line on the map corresponds to a course of constant bearing (direction), which was very useful for nautical navigation in the past (and thus made that projection very well-known).
However, from a global point of view, this projection is radically incorrect in how it shows the size of landmasses (for instance Antarctica or Greenland seem gigantic), and furthermore, it always excludes a small region around each pole (otherwise the map would be of infinite height), so it doesn't provide a complete solution for the problem of map projection. The comic implies that people who like that projection aren't very interested with map issues, and typically use what they are offered without thinking much about it.
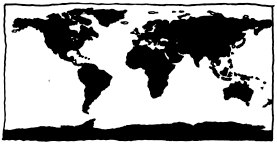
Van der Grinten
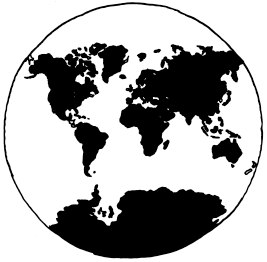
The Van der Grinten projection is not much better than the Mercator. It was adopted by National Geographic in 1922 and was used until they updated to the Robinson projection in 1988.
The Van der Grinten projection is circular as opposed to the Mercator projection. The fictional person also believes that a good projection of a three-dimensional sphere is a two-dimensional circle, which, though superficially similar, causes a vast distortion of space and area, much as the Mercator projection does. Because of this, Randall implies the Van der Grinten enthusiast to be optimistic and childishly simple-minded (e.g. "you like circles").
Robinson
The Robinson projection was developed by Arthur H. Robinson as a map that was supposed to look nice and is often used for classroom maps. National Geographic switched to this projection in 1988, and used it for ten years, switching to the Winkel-Tripel in 1998.
The Beatles was a rock band that enjoyed great commercial success in the 1960s. The Beatles, coffee, and running shoes suggest an ordinary, easygoing lifestyle paralleled by the projection.
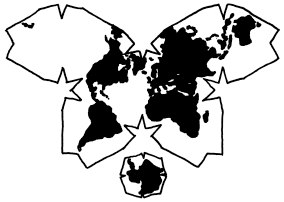
Dymaxion
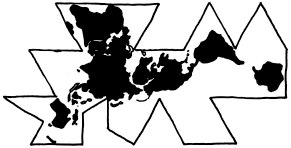
Also called the Fuller Map, the Dymaxion map takes a sphere and projects it onto an icosahedron, that is a polyhedron with 20 triangular faces. It is far easier to unwrap an icosahedron than it is to unwrap a sphere into a 2D object and has very little skewing of the poles. Buckminster Fuller was an eccentric futurist who believed, for example, that world maps should allow no conception of "up" or "down". He was therefore more than happy to defy people's expectations about maps in the pursuit of mathematical accuracy.
Randall associates the projection to geek subculture and niche markets:
- Isaac Asimov was an American science-fiction writer, that (as well as publishing many textbooks) is considered the father of the modern concept of robots. He invented the Three Laws of Robotics. He also worked on more than 500 books throughout his career.
- XML is the eXtensible Markup Language. It is used to represent data in a format that machines can read and understand, as well as being human-readable. In practice, XML is cumbersome to read.
- Toed shoes are a favorite of Randall's to pick on. In society they are seen as a geek clothing item.
- Brought to the world by Dean Kamen, the Segway PT was supposed to be a device that changed the way cities were built. In reality, most principalities have put in place rules specifically against Segways, making them a frustration to own and use within the law (in some states in Australia, it is illegal to use them on public footpaths or roads). Also, the former owner of Segway Inc., the late Jimi Heselden, accidentally rode his Segway off a cliff in 2010.
- 3D goggles are a very niche market only pursued by enthusiasts. In the 1990s the promise of virtual realities was very tantalizing; many companies attempted to perfect it, but fell short of the mark. Also, the phrase "The grass is always greener on the other side of the fence" is relevant.
- Dvorak is an alternate keyboard layout to QWERTY. According to legend, QWERTY was invented to help keep manual typewriters from jamming (by placing the most used keys far from each other) but Dr. August Dvorak performed many studies and found the mathematically optimal keyboard layout to reduce finger travel for right handed typists. While some claim Dvorak is technically better than QWERTY, QWERTY had become the standard. All the keyboards were laid out in QWERTY format, and retraining the brain after becoming a touch typist is extremely difficult.
Winkel-Tripel
Proposed by Oswald Winkel in 1921, the Winkel tripel projection tried to reduce a set of three (German: Tripel) main problems with map projections: area, direction, and distance. The Kavrayskiy projection is very similar to the Winkel Tripel and was used by the USSR, but very few in the Western world know of it.
The comic links this projection to hipster subculture. The hipster stereotype is to avoid conforming to mainstream fashions. "Post-" refers to a variety of musical genres such as post-punk, post-grunge, post-minimalism, etc. that branch off of other genres.
- Trivia
In German "Winkel-Tripel-Projektion" means Winkel's triple projection, and therefore the hyphen shouldn't be there: "Winkel Tripel" or "Winkel tripel".
Goode Homolosine
The Goode homolosine projection takes a different approach to skewing a sphere into a roughly circular surface. An orange peel can be taken from an orange and flattened with fair success; this is roughly the procedure that John Paule Goode followed in creating this projection. Randall is suggesting that people who like this map also prefer relatively easy solutions to other things in life, despite those solutions having nuanced problems that are more difficult to address.
Common people make arguments that if normal people would run the United States, then the US wouldn't be in the trouble it is. This is from the belief that career politicians are simply out to make money and will only act in the interest of their constituency when their continued easy life is threatened (usually around election time).
Airline food is another, much maligned, problem. How do you store enough food to feed people on long airplane trips? The common solution is to use some kind of sub-standard microwaveable dinner. Randall is saying that the people in favor of the Goode Homolosine wonder why the airlines don't simply order meals from the restaurants in the airport, store that food, and serve it, rather than using frozen and microwaved food.
Older cars burned oil like mad fiends, and oil back then would become corrosive to the innards of an engine, so oil had to be changed often. But, with the introduction of synthetic motor oil and better designed engines, new cars only need their oil changed about every 10,000 to 15,000 miles. A common conspiracy theory is that modern automobile oil manufacturers still recommend that car owners change their oil every 3,000-5,000 miles to "drum" up more business, even though that frequency is unnecessary.
All of these references suggest that people who like the Goode Homolosine projection are fans of easy solutions to problems. However, the solutions would not necessarily work in practice. For instance, the restaurants might have trouble making enough food for the whole plane, and it could get cold before being served. Also, the air conditions aboard planes can affect taste, so airlines say they optimize for this. And there is no such thing as a "normal" person, and if there were, he/she would have virtually no chance at actually getting into government office.
Hobo–Dyer
The Hobo–Dyer projection was commissioned by Bob Abramms and Howard Bronstein and was drafted by Mick Dyer in 2002. It is a modified Behrmann projection. The goal was to be a more visually pleasing version of the Gall–Peters.
As is discussed in the Gall–Peters explanation, the Gall–Peters was developed to be equal area, so that economically disadvantaged areas can at least take comfort in the fact that their country is represented correctly by area on maps.
Randall associates the Hobo–Dyer projection to "crunchy granola" — a stereotype associated with vegetarianism, environmental activism, anti-war activism, liberal political leanings, and some traces of hippie culture.
With the new general acceptance of homosexual, bisexual, and transgender persons, some have begun to invent gender-neutral pronouns so that when referring to a person whose gender is not known they cannot be offended by being referred to by the wrong pronouns. In Middle English 'they' and 'their' were accepted gender-less pronouns that could replace 'he', 'she' as well as be used to represent a crowd, but this usage is considered by some to be grammatically incorrect because of the plural/singular debate (stupid Victorian Grammarians!). None of the many attempts at popularizing gender-neutral pronouns have achieved any degree of success in the mainstream.
Plate Carrée
Also known as the Equirectangular projection has been in use since, apparently, 100 AD. The benefit of this projection is that latitude and longitude can be used as x,y coordinates. This makes it especially easy for computers to graph data on top of it.
According to the comic, the projection appeals to people who find much beauty in simplicity.
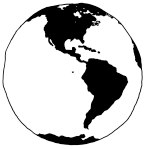
A Globe!
In any good discussion there has to be at least one smart-ass. This is a comic about map projections, that is, the science of taking a sphere and flattening it into 2 dimensions. The smart-ass believes that we shouldn't even try: a sphere is, tautologically, the perfect representation of a sphere.
To quote The Princess Bride: "Yes, you're very smart. Shut up."
Waterman butterfly
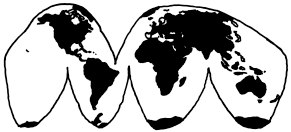
Similar to the Dymaxion, the Waterman butterfly projection turns a sphere into an octahedron, and then unfolds the net of the octahedron, which was devised by mathematician Steve Waterman based upon the work of Bernard J.S. Cahill.
Bernard Cahill published a butterfly map in 1909. Steve Waterman probably has the only extant "ready to go" map following the same general principles, though Gene Keys may not be far behind. Waterman has a poem with graphics in a similar vein to this xkcd comic that is worth reading.[1]
Polyhedral projections like Cahill, Dymaxion or Waterman typically offer better accuracy of size, shape and area than flat projections, at the expense of compass directionality, connectedness, and other complications.
The joke is that the person responding deeply understands map projections; anyone who knows of this projection is a person that Randall would like to get to know.
Peirce quincuncial
The Pierce quincuncial projection was devised by Charles Sanders Peirce in 1879 and uses complex analysis to make a conformal mapping of the Earth, that conforms except for four points which would make up the south pole.
Inception was a 2010 movie about meta lucid dreaming. It has a complex story that is difficult to follow and leaves the viewer with many questions at the end, and almost needs to be watched multiple times to be understood.
The human brain is not well developed to deal with oddly obvious things. One example is that everyone has a skeleton, but everyone is surprised to see a part of their body represented by an X-Ray. Another is the fascinating complexity of the human hand, a machine which is amazingly complex, driven by a complex interplay of electrical and chemical signals; yet is the size of the hand and so useful.
Gall–Peters
The Gall–Peters projection is mired in controversy, surprising for a map. James Gall a 19th century clergyman presented this projection in 1855 before the British Association for the Advancement of Science. In 1967, the filmmaker Arno Peters created the same projection and presented it to the world as a "new invention" that put poorer, less powerful countries into their rightful proportions (as opposed to the Mercator). Peters played the marketing game and got quite a few followers of his map by saying it had "absolute angle conformality," "no extreme distortions of form," and was "totally distance-factual" in an age when society was very concerned about social justice. All of these claims were in fact false. The polar regions are horribly distorted, and south of the Mediterranean Sea is "taller" than it should be.
Anyone who loves such a politically charged map that has become popular by way of marketing stunts, Randall would rather not have anything to do with.
Title text
The title text makes a joke that goes to the familiar meme from CSI: Miami, in which the star, David Caruso starts a sentence, then puts on his sunglasses and ends the sentence with a corny pun. In this case, the pun is on map projection and projection in Psychology. Psychologic projection is an immature defense mechanism wherein a person who is uncomfortable with their own thoughts and/or actions assumes that another also shares this thought or action and blames that person for thinking/behaving that way, removing some of the negative feelings they have towards themselves. The Sunglasses internet meme has been mentioned previously by xkcd in comics 626, 524 and possibly others.
Transcript
- What your favorite
- Map Projection
- says about you
- [All of these are organized as Title, a copy of the particular projection underneath, and what it says about you under that.]
- Mercator
- You're not really into maps.
- Van der Grinten
- You're not a complicated person. You love the Mercator projection; you just wish it weren't square. The Earth's not a square, it's a circle. You like circles. Today is gonna be a good day!
- Robinson
- You have a comfortable pair of running shoes that you wear everywhere. You like coffee and enjoy The Beatles. You think the Robinson is the best-looking projection, hands down.
- Dymaxion
- You like Isaac Asimov, XML, and shoes with toes. You think the Segway got a bad rap. You own 3D goggles, which you use to view rotating models of better 3D goggles. You type in Dvorak.
- Winkel-Tripel
- National Geographic adopted the Winkel-Tripel in 1998, but you've been a W-T fan since long before "Nat Geo" showed up. You're worried it's getting played out, and are thinking of switching to the Kavrayskiy. You once left a party in disgust when a guest showed up wearing shoes with toes. Your favorite musical genre is "Post–".
- Goode Homolosine
- They say mapping the Earth on a 2D surface is like flattening an orange peel, which seems enough to you. You like easy solutions.You think we wouldn't have so many problems if we'd just elect normal people to Congress instead of Politicians. You think airlines should just buy food from the restaurants near the gates and serve that on board. You change your car's oil, but secretly wonder if you really need to.
- Hobo-Dyer
- You want to avoid cultural imperialism, but you've heard bad things about Gall-Peters. You're conflict-averse and buy organic. You use a recently-invented set of gender-neutral pronouns and think that what the world needs is a revolution in consciousness.
- Plate Carrée (Equirectangular)
- You think this one is fine. You like how X and Y map to latitude and longitude. The other projections overcomplicate things. You want me to stop asking about maps so you can enjoy dinner.
- A Globe!
- Yes, you're very clever.
- Waterman Butterfly
- Really? You know the Waterman? Have you seen the 1909 Cahill Map it's based— ...You have a framed reproduction at home?! Whoa. ...Listen, forget these questions. Are you doing anything tonight?
- Peirce Quincuncial
- You think that when we look at a map, what we really see is ourselves. After you first saw Inception, you sat silent in the theater for six hours. It freaks you out to realize that everyone around you has a skeleton inside them. You have really looked at your hands.
- Gall-Peters
- I hate you.
- Mercator
Discussion
I have a Plate Carrée hanging on my wall myself. Never failed me yet. Davidy22[talk] 07:05, 2 February 2013 (UTC)
I like the Azimuthal Equidistant (equatorial aspect) the best. - not Pennpenn. 108.162.221.43 01:15, 17 December 2015 (UTC)
You can explore and compare different map projections and their distortions (using Tissot’s indicatrix and triangulation of sphere) in an interactive blog post The problem with maps by Michael Davis --JakubNarebski (talk) 14:58, 26 May 2017 (UTC)
Go check out that site carefully though most of the data is accurate, some of the media is not, for example the two side by side Google maps satellite images of cars and the text saying how a map projection changes the apparent size of the cars. Well if you open up both links you will see they are at different zoom levels, one at a scale of 50 feet per unit and the other at 100 feet so yes being twice the zoom the cars are going to appear larger then the image right next to it. 162.158.62.231 12:04, 23 August 2017 (UTC)
Btw, this comic is given in What Does Earth Look Like? of Vsause where these projections are discussed. --Ата (talk) 10:38, 3 September 2017 (UTC)
- Dymaxion
Dymaxion is clearly the best. There's nothing like a map made out of an unfolded d20. Alpha (talk) 19:43, 23 February 2013 (UTC)
- Makes you wonder what if a dodecahedron had been used instead of an icosahedron. --Quicksilver (talk) 18:02, 17 August 2013 (UTC)
- Here you go: http://www.progonos.com/furuti/MapProj/Normal/ProjPoly/Foldout/Dodecahedron/dodecahedron.html - Frankie (talk) 16:40, 23 July 2015 (UTC)
- Oh noes, Progonos map site has shut down. Alternatives: http://www.csiss.org/map-projections/Miscellaneous.html and https://lynceans.org/all-posts/polyhedral-projections-improve-the-accurately-of-mapping-the-earth-on-a-2d-surface/ - Frankie (talk) 23:14, 11 July 2019 (UTC)
- Quincunx
Peirce Quincuncial has 4 non-conformal points, but not the 4 corners, which are the south pole, but instead are the 4 midpoints of the sides. These are on the equator and seem to be 90 degrees apart.--DrMath 06:30, 30 August 2013 (UTC)
- I love Peirce Quincuncial, yet I slept throughout that "Inception". 141.101.99.228 11:36, 27 January 2014 (UTC)
- I'm surprised nobody thought of "really looking at your hands" as a hint that person that likes this projection is under influence of LSD or similar drug. As this surely is a thing that you do. (and you'll think of it next time you smoke your joint - inception!) --108.162.254.137 17:29, 7 December 2014 (UTC)
Plus it has a picture of a man looking at his hand and a man looking at the man looking at his hand. I used Google News BEFORE it was clickbait (talk) 14:39, 22 January 2015 (UTC)
xkcd 1051's title text - "meta lucid dreaming". I really got excited that there was an article about and ironically, it leads to meta and lucid dreaming separately. 173.245.55.67 21:23, 25 March 2014 (UTC)BK201
The common video game trope of "the far east of the world is connected to the far west, and the far north likewise to the far south" is popularly resolved by saying that those game worlds are toroidal shapes. (For a particular reference, I am thinking of the SNES and PSX era Final Fantasy games (4-9.)) But sometime in the last year, I got the idea that you could also resolve that geographical conflict (and claim they are spherical) by the logic that the "world map" you see in those games (where they have one) is a Peirce Qunincuncial map. Is my logic sound? Boct1584 (talk) 15:31, 28 March 2015 (UTC)
The explanation for the Peirce Quincuncial seems to miss the fact that Randall is implying that anyone who likes this map is most likely high. Getting lost in deep thought over things like your hands, or sitting in a dark theater for 6 hours to wrap your head around Inception...these are all very stereotypical "has smoke a lot of marijuana" behaviors. 108.162.216.21 (talk) (please sign your comments with ~~~~)
The Quincuncial map is one of few maps that can tile infinite plane such that any 2 arbitrarily close points on the plane correspond to 2 arbitrarily close points on globe and vice versa.
- Waterman
In actual fact, the Waterman butterfly map used a truncated octahedron based upon the mathematics of close packing of spheres and is not at all based upon any of CaHill's work/math. -- steve waterman 65.92.20.61 (talk) (please sign your comments with ~~~~)
- Perhaps the explanation should mention that Waterman himself signed up at forum.xkcd.com and vigorously denied that his map has anything to do with Cahill. At the time, it was unclear whether the account was really Waterman, or just a troll trying to make him look bad. - Frankie (talk) 21:39, 25 March 2014 (UTC)
What makes the Waterman butterfly map better than the Goode Homolosine map? The downsides of the Goode Homolosine map listed can both apply to the Waterman map: the oceans are all cut up in both of them, and while Greenland is safe in the Waterman butterfly, the edge of Asia gets sent over to North America’s wing. tsuchinoko real (talk) 02:57, 29 January 2024 (UTC)
- Kavrayskiy VII
Kavrayskiy is the best projection, despite being so far out of the mainstream that no-one west of Ukraine has seen one for the past 20 years. 173.245.54.64 (talk) (please sign your comments with ~~~~)
- Wow, I looked into it and it really seems like an excellent projection. It's been a while since I've looked at projections but I think it's my new favourite as it has everything that I've been looking for in a projection. It's a more accurate (in extremes) and more pleasing Robinson projection that still has a reasonable amount cut off the top. Also, the indicatrix for it is very simple, as is the formula, and simple things please simple minds (like mine, apparently) -- without taking it to an extreme like the equirectangular projection does. I swear I've come across it before, but then again I grew up in a country which wasn't far from the Eastern Bloc. 141.101.98.214 14:51, 5 November 2014 (UTC)
- Sphere
To be fair, what is drawn is an orthographic azimuthal projection.--108.162.216.153 18:59, 14 December 2014 (UTC)
GLOBES ARE THE BEST although my enormous Winkel Tripel hasn't done too bad. 108.162.219.9 (talk) (please sign your comments with ~~~~)
Airline food is never microwaved, and is chilled rather than frozen. Also the problems aren't limited to storage and re-heating, there are technical considerations with low air pressure, dehydrated air etc. and concerns over strong smells. I edited the relevant section. AmbroseChapel (talk) 07:00, 11 September 2017 (UTC)
"Here is what it says about you" is a common phrase in online personality quizzes, pages and other things. 162.158.167.234 (talk) (please sign your comments with ~~~~)
Randall Hates New Zealand. Koro Neil (talk) 03:40, 7 January 2019 (UTC)
Isn't the "skeleton inside" thing a reference to Ray Bradbury's "The Skeleton" Shadowsapex (talk) 08:32, 27 January 2019 (UTC)
Wording disagreement
Loodog and I disagree about the wording of the Peters map explanation.
The previous version of the text (written by LCarsos in 2012):
- Anyone who loves such a politically charged map that has become popular by way of marketing stunts, Randall would rather not have anything to do with.
Loodog's version of the text:
- The implication is that the fans of this map are pompously concerned with social justice, and willing either to lie or convey marketing mistruths to promote that cause.
I believe Loodog's wording is excessively non-neutral, and the old wording should be restored. - Frankie (talk) 19:29, 20 November 2019 (UTC)
- FWIW, I disagree that Peters fans are "pompously concerned with social justice". IMO, they are just assholes who enjoy using the terminology of social justice as their cudgel. People who genuinely care about social justice don't use Peters.
- Amnesty International, Human Rights Watch, and the International Organization for Migration are three of the world's largest social justice organizations. Each of them has been described as "pompous" by detractors. [2] [3] [4] None of them use Peters map projection. [5] [6] [7] AI & HRW use a mix of Hobo-Dyer, Equirectangular, and probably Mercator. IOM uses something rounded (probably Robinson or W-T), Equirectangular, and Mercator. - Frankie (talk) 19:34, 20 November 2019 (UTC)
- I'm inclined to agree; certainly we should be careful about calling people "pompous" in the article voice. I went back to the older wording but added "...and false claims..." after marketing stunts, which seems to have been the main thing that the person who changed it objected to and which can be stated more neutrally like that. --Aquillion (talk) 07:13, 9 January 2023 (UTC)
Hemispheric Interrupted Mollweide
Still disappointed that Randall didn't include the BEST projection: Interrupted Mollweide Hemispheres. It combines key aspects from the clean math of Equirectangular, the values of Hobo-Dyer, the circularity of Van Der Grinten, the flattening of Homolosine, and the hipness of Winkel Tripel. - Frankie (talk) 15:09, 31 October 2022 (UTC)
- Maybe next time While False (museum | talk | contributions | logs | rights) 19:00, 31 October 2022 (UTC)
i like peirce quincuncial and plate carree (bonus points the fact it's the oldest one). mercator is a bit meh, but let's give it credit for being one of the first projections (in fact it is the second oldest projection). gall-peters is the ugliest projection i've seen, and hobo-dyer is second ugliest. the butterfly one is also good but a bit weird, and the ichosaedron one that i forgot the name is... weird. like, wtf is that, it doesn't even look like a map, idk, where's europe there An user who has no account yet (talk) 18:31, 6 September 2023 (UTC)
- For the "icosahedron one", you mean the Dymaxion? In which case, Europe is in the topmost trapezoid (left, as opposed to the two triangles top-right). See Africa (Madagascar crossing an edge) in one corner, see the 'squiggle' of the Med and then Europe (rotated maybe 150 degrees over) crammed in the right of the extrusion. 172.71.242.76 21:47, 6 September 2023 (UTC)
Projection
It should maybe be explained that the concept of determining what someone's personality is like by what map they prefer is itself projection -- Mesoseven (talk) 05:20, 3 January 2024 (please sign your comments with ~~~~)
- Might be worth disambiguating/adding to the projection (psychology) link in the Title Text section. I mean, they're not totally the same thing, but could be dealt with together with the right wording. (PS, I shuffled/reformatted your contribution. You did 'sign', but not sign, and you can check the layout of the handy wikilink template we use here if you read how I've made your link; and my own without any replacement text. Welcome to the wiki, and if you have any questions...) 172.70.90.173 07:30, 3 January 2024 (UTC)
- Image placement
I'm torn, which is better?
--FaviFake (talk) 18:41, 5 May 2025 (UTC)
Should someone revisit the explanation of gender-neutral pronouns? The various new ones people are coming up with are generally used to describe their own personal experience with gender, while people who are talking about an unknown person, i.e. "oh, look, someone dropped their sunglasses in the river", are probably not going to be using any sort of new pronoun because the word "they" is right there. For that matter, whoever's saying that is probably not using the word "they" to avoid hypothetically offending whoever dropped sunglasses in the river, but saying it because "someone dropped his or her sunglasses in the river" is sort of awkward to say and just saying "his sunglasses" or "her sunglasses" is a tad odd when the person's gender isn't known.
(something something "also you'd have to say 'someone dropped his, her, or their sunglasses' due to not everybody being a him or a her in the first place" something something good phrasing.)
I'd also understood "you use a recently-invented set of gender-neutral pronouns" to mean "you use those pronouns /for yourself/", rather than declaring what pronouns the person in question uses for another person of unknown gender, so I'm not sure that how people refer to others is relevant at all? 74.192.155.229 14:04, 18 August 2025 (UTC)