3189: Conic Sections
| Conic Sections |
 Title text: They're not generally used for crewed spacecraft because astronauts HATE going around the corners. |
Explanation
|
This is one of 63 incomplete explanations: This page was created by a section through a scone. Don't remove this notice too soon. If you can fix this issue, edit the page! |
A Kepler orbit describes the simplified motion of two celestial objects around each other. Such an orbit will form a conic section. A conic section is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though it was sometimes considered a fourth type. In reality, this model is based only on their basic gravitational forces and ignores any other factors such as the gravity of other objects, atmospheric drag, each object being a non-spherical(/non-point) body of non-uniform density and any relativistic effects, but it serves as the basis for most orbital calculations before further refining with the most relevant additional perturbations.
In real conic sections, the cone extends to infinity. In the comic, however, the "conic section" representing the satellite's orbit has been assumed to have a base at a distance that inconveniently crosses the indicated orbital path (that might be assumed to be eliptical, otherwise), resulting in sharp corners where the angled planar section through the cone meets that base. As alluded to in the title text, these corners would be extremely uncomfortable for an astronaut in a crewed spacecraft. Such an extreme and sudden change in direction would require a very large, potentially dangerous, G-force.
Being in a free orbit necessarily means following an ellipse (or very similar, outside of the mathematically strict two-body problem) in which there is net zero acceleration, combining the pull of gravity and the forces that would be felt due to the continually changing direction alone. Being forced off this ellipse to move across the totally imaginary and arbitrary conic-base would force an instantaneous acute change of direction for no other reason than to follow the imperfectly understood mathematical 'model' at two arbitrary points (reaching the baseline and rejoining the true curve again), which would technically require infinite acceleration each time.
Alternately, deliberately 'cutting the corner' of an orbit would require the best effort of the spacecraft to stick to the truncated-orbital path, requiring as much thrust by the craft as it can muster (which any occupants would have to endure), including along the less uncomfortable but still forceful passage along the 'straight' bit of the orbit through the curved space-time of the gravitational field of the parent body. We also aren't given any indication of how the 'radial' velocity might be intended to change during the 'flat' phase, such as if it obeys the same constant 'area sweeping' rule as for the elliptic part of the path.
Transcript
|
This is one of 35 incomplete transcripts: Don't remove this notice too soon. If you can fix this issue, edit the page! |
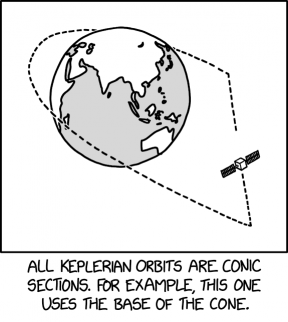
- [A view of the Earth, focused on Asia and the Indian Ocean with East Africa at left and the Western Pacific and Australia at right. A satellite is shown in an unusual orbit around the planet.]
- [Caption below the panel:]
- All Keplerian orbits are conic sections. For example, this one uses the base of the cone.
Add comment 
Create topic (use sparingly) 
Refresh Discussion
Isn't the base of a cone, just a circle? How would this have "corners"? SDSpivey (talk) 01:41, 3 January 2026 (UTC)
- The cone upon which a conic section exists doesn't actually have a base, it's just arbitrarily large (possibly infinitely so) in order for the section to only ever lay along the 'curve' of the cone part.
- But, here, the base is wwhere you give up on plotting how far 'down the cone' you go, of the sufficiently large ellipse (or possibly parabolic/hyperbolic curve), which is indeed round but has an sharp (i.e. acute) angle between its flat (and incidentally circular) plane-section and the 'wrapped' pseudo-euclidean plane of the conic-section it intersects with. 92.23.2.208 01:50, 3 January 2026 (UTC)
Bring a jacket and spoon for orbits that go through the ice cream.Lord Pishky (talk) 01:43, 3 January 2026 (UTC)
I'm pretty sure this is the shape of the flat bottom of a cake cone. 71.212.56.254 03:02, 3 January 2026 (UTC)
- They REALLY hate the flat-bottom cone orbits and the waffle cones make for a bumpy ride.Lord Pishky (talk) 18:57, 3 January 2026 (UTC)
It appears to be a cut-off section of an ellipse, so basically a regular orbit with a sharp line. (Desmos) Tanner07 (talk) 04:29, 3 January 2026 (UTC)
https://media.licdn.com/dms/image/v2/D5622AQH3CYoPXy1cqg/feedshare-shrink_2048_1536/feedshare-shrink_2048_1536/0/1727242249609?e=1769040000&v=beta&t=UdAX9TH3joo-vpvj4pRWXoCQyF6JVUPVmyONWghcj5E --PRR (talk) 05:06, 3 January 2026 (UTC) Add comment
