2286: 6-Foot Zone
| 6-Foot Zone |
 Title text: Technically now it's a 34-foot zone. |
Explanation
| |
This explanation may be incomplete or incorrect: Created by 8 HORSES. Please mention here why this explanation isn't complete. Do NOT delete this tag too soon. If you can address this issue, please edit the page! Thanks. |
This comic is the 11th comic in a row in the series of comics about the 2020 pandemic of the coronavirus - SARS-CoV-2.
This comic is about social distancing, a common practice to prevent the spread of the COVID-19 disease. It has been suggested to maintain 6 feet (i.e. 1.83 m - in countries with SI units it is 1.5 m) of distance between yourself and other people, to prevent the transmission of respiratory droplets from you to others (or vice versa).
Randall takes this 6 feet of distance, and does calculations of the "area" of distancing, "border", population density, and "real estate value". With 6 feet of distance, these calculated variables are incorrect. Besides the radius of the body, only a radius of 3 feet has to be taken into account for a distance of 6 feet between two people. He finally culminates in determining the number of horses that could also fit in the space.
Randall's border length and approximate area calculations are based on a zone with an outside radius of approximately 6.8 feet or 82 inches (2.07 m), meaning that the person has a radius of approximately 0.8 feet or 10 inches (0.24 m).
The title text is a pun using the alternate definition of foot, noting that a human has two feet and a horse has four, so 8x4 + 2 = 34 feet.
Transcript
| |
This transcript is incomplete. Please help editing it! Thanks. |
- Guide to the 6 foot Social Distancing Zone
- Profile image of person with 6 foot distance measurements on both sides
- Overhead image of person within a roughly circular shape extending 6 feet in all directions from the person. The dimensions of the person account for the non-circular shape.
- Approximate area: 145 square feet
- Border length: 43 feet
- Population density: 190,000 people/square mile
- Value at NYC real estate price per square foot: $195,000
- Maximum number of horses that could fit inside it with you, estimated using the dimensions in the US Forest Service Equestrian Design Handbook: 8
Discussion
Ok... 34 feet, in total, but how many hands? (All of which you should wash!) 162.158.34.210 23:34, 27 March 2020 (UTC)
Well, a typical horse stands 15.2 hands tall. You do the math. Cellocgw (talk) 01:09, 29 March 2020 (UTC)
- Love it. Given the extra 1.7 feet for the person, a radius of 20.53 hands. If it were just 6 feet, 18 hands -- brad --108.162.216.122 00:55, 28 March 2020 (UTC)
- For a horse of 16 hands (from the USFS document), 130 hands (8x16 'hands' + 2 hands). Or 123 and three loose fingers using Cellocgw's value, with that sounding like it's from actual practical experience. 162.158.89.49 19:09, 29 March 2020 (UTC)
So Randall is figuring about 1.7 feet diameter for the person. --172.68.174.70 00:40, 28 March 2020 (UTC)
The 190,000 people / mile^2 assumes (I'm guessing) flat ground. Skyscrapers make a difference [citation needed] -- brad --108.162.216.122 00:55, 28 March 2020 (UTC)
Interesting that the population density he gives ignores circle packing. Population should be 174,000. -- coyne -- 162.158.122.156 04:06, 28 March 2020 (UTC)
- Circle packing is unimportant since he's just giving the population of this one circle. He's taking a radius of 6 foot around that person without specifying what he considers to be the radius of the person, but it can be inferred from the numbers:
from area: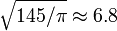 ,
,
from circumference: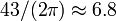 ,
,
from population density: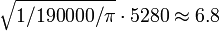 ,
,
so apparently he considers a person to have a radius of 0.8 ft, or about 0.5 m diameter, which seems reasonable. Zmatt (talk) 05:11, 28 March 2020 (UTC) - Note that even if you want to know the population of optimally packed people, your number is still wrong since the circles overlap: your circle is supposed to exclude other people, it doesn't exclude other people's circles. Optimally you'd have a triangular lattice of people with a lattice distance of 7.6 ft (assuming we want 6 ft between people and we consider people to be circles of radius 0.8 ft). This yields a population density of 1 person per
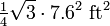 , which is about 1.1 million people per square mile. Zmatt (talk) 05:24, 28 March 2020 (UTC)
, which is about 1.1 million people per square mile. Zmatt (talk) 05:24, 28 March 2020 (UTC) - But some people still live in cities. So they are not packed 2-dimensional but sometimes in very high skyscrapers. We need to bringt globes into this calculation instead of circles. --Lupo (talk) 06:40, 30 March 2020 (UTC)
Much as I love thinking about circle packing density in the plane, I think the above explanation is slightly overthinking the issue. The population density figure appears to be using the idea that one person's zone contains one person; 1 person / (145 ft^2) does indeed equal 192,000 people/square mile. So, he's not saying that 'given these constraints, we can pack people at this maximum density'. He's saying 'given this area, and counting it as a tiny sovereignty, we can calculate its population density to be this'. For this reason, I don't think you should say that the 'population density' figure has an error, only that it is calculated in a different sense than you were thinking about. Dextrous Fred (talk) 18:58, 28 March 2020 (UTC)
- I agree. My first instinct on what the population density figure means was the same as one used in the comic. 162.158.103.163 22:29, 28 March 2020 (UTC)
Possibly a play on the fact that horses are measured in hands? --orbitalbuzzsaw--
Page 207 of US Forest Service Equestrian Design Guidebook for Trails, Trailheads, and Campgrounds says minimum corral size is 12x12 feet. I didn't find a more likely sounding Forest Service publication. So I assume the handbook in the comic is a fictional publication. Hamjudo (talk) 13:15, 28 March 2020 (UTC)
- Don't look for corrals. Look for how are you supposed to pack the horses for traveling eg. in train or truck/trailer. -- Hkmaly (talk) 00:22, 29 March 2020 (UTC)
Always knew cities were bad for humanity. As are airplanes. Need them both to create a pandemic. Seebert (talk) 18:32, 28 March 2020 (UTC)
Thanks for that explanation! When I saw the title text, I was worried that WHO had increased the recommendation and I'd missed it. TobyBartels (talk) 00:47, 29 March 2020 (UTC)
Cool. I didn't know the US Forestry Service designed horses. These Are Not The Comments You Are Looking For (talk) 06:00, 29 March 2020 (UTC)
Should it be noted that Randall used horses as units of measurement and/or as reference objects before? i.e. 1461 Elektrizikekswerk (talk) 08:52, 30 March 2020 (UTC)
I'm relatively surprised that nobody is discussing the 'real estate' value in these comments. I guess I'm the odd one out. The value of $195k was, to my surprise, very accurate. Zillow.com currently lists that the average real estate price per square foot in Manhattan is $1,371, which, when multiplied by Randall's approximate 145 square feet, gives $198,795. I can't believe the rest of you are putting this much research into horse dimensions. 162.158.75.4 23:55, 30 March 2020 (UTC)
- I'm with you, there should be a comment on that reference to NYC Real Estate. I wasn't too sure about how, exactly, to do the math. The Real Estate market actually has those 145 square feet stacked up, so I was thinking about 145 square feet of _land_, but the zillow numbers are for 145 square feet of _floor_. Since your numbers work out, that probably means Randall was going for that reading. MAP (talk) 03:38, 31 March 2020 (UTC)
- But of course, NYC is not only Manhattan; i'm pretty sure that the rest of the city is cheaper. 172.68.51.94
