3125: Snake-in-the-Box Problem

Snake-in-the-Box Problem

|< < Prev #3125 (August 6, 2025) Next > >|

Title text: Chemistry grad students have been spotted trying to lure campus squirrels into laundry hampers in the hope that it sparks inspiration.

|< < Prev Random Explanation Next > >|

Explanation

This is one of 52 incomplete explanations: This page was created recently by Schrodinger's snake. Don't remove this notice too soon. If you can fix this issue, edit the page!

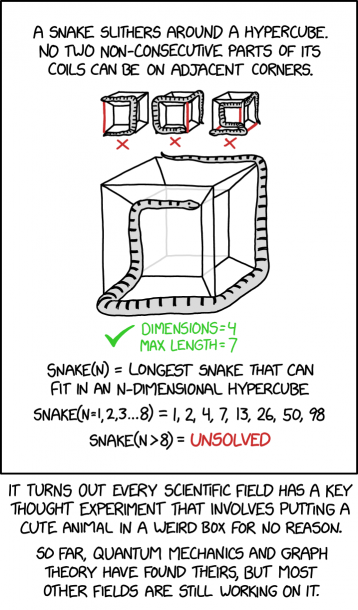
This comic makes fun of the fact that many fields of science use analogies to help visualise complex problems. One such analogy (drawn in the comic). Involves a snake in a hypercube.

Graph theory has a thought experiment involving a snake on the edges of an n-dimensional hypercube.

The other thought experiment referred to is the Schrödinger's cat, which is used in quantum physics. In this experiment, a cat is put in a box which contains poison and a Geiger counter, which absolutely fits the definition of a stange box.

Transcript

This is one of 27 incomplete transcripts: Don't remove this notice too soon. If you can fix this issue, edit the page!

  Add comment        Create topic (use sparingly)       Refresh 

Discussion

The math problem in question is https://oeis.org/A099155 Mei (talk) 21:57, 6 August 2025 (UTC)

why is d>8 unsolved? stevethenoob 21:59, 6 August 2025 (UTC)

Computational power, I guess, although I'm going to go out on a limb and predict that for N=9 snake=196. 94.73.52.245 23:18, 6 August 2025 (UTC)

It's not that hard to imagine: if you were to try a brute force search it would take time that's exponential in the path length, which itself is exponential in d. There are evidently methods to do it slightly better, but not enough to make solving d=9 feasible yet. Zmatt (talk) 10:03, 7 August 2025 (UTC)

To give an impression of the rate at which these get solved: d=6 was solved in 1988, d=7 in 1996, d=8 in 2014. Zmatt (talk) 10:32, 7 August 2025 (UTC)

Computational power is right. Time complexity is *super*-exponential - even the number of *nodes* increases exponentially as increasing N by 1 doubles the nodes. And time complexity doesn't increase linearly with the number of nodes - if we imagine a brute force algorithm there's 2^n nodes and each node has n-1 options, so we're looking at a multiple of exponential time. Current lower bound for N=9 is 190. GorillaWarfare (talk) 06:57, 10 August 2025 (UTC)

I would argue that computer science has one as well with the China room problem. Ctinsman (talk) 22:14, 6 August 2025 (UTC)

Humans aren't cute animals (mostly), so I propose a variant of the problem called the Chinese Red Panda Room 177.12.49.23 22:38, 6 August 2025 (UTC)

Interesting. Just a few days ago I was investigating a very similar idea (looking at a path that transitioned between adjacent faces of a polyhedron, which was effectively going from vertex to connected vertex upon that chosen polyhedron's dual), but for the opposite reason, i.e. looking for the paths that actually maximised proximity (along the path) between neighbouring faces (upon the polyhedra), so that it actually minimised the search back/forth along the path-chain to establish what value the adjacent polyhedron faces (beyond the ones automatically at ±1 positions on the chain) inherited.
As to solving this one (basically disallowing visiting of any nodes adjacent to prior visits other than the single one that the +1 position of the chain has to first go to), I've got a basic idea of how I'd N-dimensionally space-search the possible routes (after all, visiting any given node at {0,1} value for dimensions [a, b, c, ...] rules out now visiting all of [!a, b, c, ...], [a, !b, c, ...], [a, b, !c, ...], etc, except whichever one of these was chosen for the next step of onward travel), for valid foldings across the appropriate N-polytype cuboidal analogue. Though I suspect that the exponental (or greater!) growth in the potential search-trees you'd use would be the sticking point. No point in setting off an exhaustive algorithm if it seemed likely to take three years to check just 1% of possibilities, and no doubt more dedicated analysis than my own brute-forcing method has already hit other problems in trying a more nuanced extrapolation between each level of added dimensionality, which is where the unsolved nature of this starts to bite.
But also think it'd be far more interesting to investigate the possibilities in the N>3-Dimensional extensions of non-cubic platonic solids, like the 600-cell and beyond, and establish what allowable lengths of traversal they would allow, under similar stipulations.
Great! I love getting things like this to think about. If I can spare the time needed... 82.132.245.59 22:22, 6 August 2025 (UTC)

I think you've been nerd-sniped. 177.12.49.23 22:42, 6 August 2025 (UTC)

So far, I've personally got as far as:

• For any given number of dimensions, N, there are always N adjacent points (point, zero dimensions, zero neighbours; line, one dimension, one neighbour; square, two dimension, two neighbours, etc).
• In total, there are 2^N points (0d=1, 1d=2, 2d=4, etc)
• A maximum possible length, L, has a lower lower limit of starting at any particular vortex and only taking directions that are perpendicular to all prior directions (for a cube, only go by x, y and z directions once), and this would be eaual to N.
• But that's overly-lazy, as you're ruling out (as you gain enough dimensions) revisiting a dimensional plane, even though you're allowed to revisit a point on that plane that's shifted by at least two other dimensions of offset. e.g. the top right of a cube's facing face when you started at the bottom left of it (went 'deep' to the rear face, took two steps from the rear-lower-left to rear-upper-right then back).
• For the first step, you have N choices from your starting position. You take one and cannot later visit any of the ones you did not choose to go to. For the second step onwards, you have N-1 basic choices (every direction but backwards to the prior step) and should choose one and rule out ever visiting the rest.
• This gives a new (at least for N>2) lower limit to L whereby the sum of starting, taken and not-taken nodes that you count can be added to by new steps until you would end up with have a total greater than 2^N. (Line: start on one (of two), choice of one (taken), two points 'marked', only two points possible; Square: start on one (of four), two choices, take one, reserve one, three points 'marked', still the fourth point available for L=2, but then five points would be marked (the untaken-from-start being the only non-backwards choice) so can't go further.
• But this is also wasteful as (in increasingly higher dimensions) there's nothing to stop an unvisited neighbour of a past step from being a(n enforced) unvisited neighbour from a later step, as you 'choose' to go only to a valid further point. So clever "near-neighbour" backtracking can reduce the number of freshly eaten-up points and thus maintain more future points for more steps.
  • Noting that past-step no-go-neighbours that can possibly 'fold into' the current-step's not-going-neighbours list only become such after at least two intervening steps (for 'square-based' hypercubic domains, whereas triangle-based hypernets (e.g. tetra-, octa- and icosohedrons, in 3-space) happen after just one step, and pentagon-based ones (dodecahedrons in 3-space) can't take advantage of this in less than three. (This seems to share some of the mathematics with the 'classical' rabbit-population problem, whereby new offspring only become viable breeding population after a step or two since their generation.)
• Optimally, in fact, you should aim to double-back in such a way as leave yourself with all but one onward neighbour unavailable (thus only eating up potential points at a rate of one per step, at that point).
• Heading vaguely back 'towards' past snake-lengths, in higher-dimensional hypernets, seems like the best(/longest) space-filling strategy. It's a bit like coil-built pottery, but with more undulations (and dimensions) to it. But with care to make sure you don't burrow yourself into a dead-end with no viable onward choices while still having maybe half of the potential visitable/neighbourable points untouched, or avoiding filling 'voids' to guaranteeing accessing a majority of the potential future visits, but unwisely not exploiting all the phase-space of vertices optimally.
  • I can mentally visualise doing this successfully in 3-, 4- and 5-cube situations, elegantly enough (it's like , but N>=6 versions get increasingly hard to do in my head with certainty. After I've slept on it, I might have to break out the pencil and paper.

So, yeah, I've set a lower-limit to L, for various Ns, and can construct a possible upper-limit to L, but I haven't even checked these L(N)s vs. the values stated in the comic. Or what progress (and more advanced logical reasoning) has already been made in the field. I suspect I'm just reinventing the (hyper-)wheel, of course, rather than have the key to the problem that everyone else had failed to spot, but that's not the point. If I get even half way close to what the 'professionals' in this field have managed, I'll be smug and self-satisfied enough for myself. And, anyway, I've explained myself enough tolet any other similarly-minded nerd the ability to get at least as far as I've got with this problem. Which is as good an outcome, as far as I'm concerned, as getting this done entirely on my own. 82.132.244.41 00:33, 7 August 2025 (UTC)

I'm still having trouble getting hold of long enough snakes. 82.13.184.33 08:31, 7 August 2025 (UTC)

I've got the 50 length one for 7D, lets see if I can go further :) --Darth Vader (talk) 13:25, 7 August 2025 (UTC)

Psychology is way ahead of y'all, they've been putting actual mice in weird boxes for decades. 177.12.49.23 22:45, 6 August 2025 (UTC)

Psychology might have been putting animals in boxes for decades, but zoology has been doing it for centuries! 97.118.209.207 00:36, 7 August 2025 (UTC)

Gastronomy has been doing it for as long as people have been storing food. BunsenH (talk) 03:41, 7 August 2025 (UTC)

https://scratch.mit.edu/projects/284912743/--2001:4450:8178:2200:D1C2:8DED:F6FE:E93C 04:01, 7 August 2025 (UTC)

That link doesn't work. When I remove the -- at the end it goes to some kind of math game. Barmar (talk) 15:58, 7 August 2025 (UTC)

Reading (just) the [comments] of the underlying research suggests that 98 is the longest found snake. Perhaps that means a longer one has not been explicitly eliminated (making 8 also not solved to some extent) 2A02:A45B:8867:0:BED8:F2BA:838E:765 22:52, 6 August 2025 (UTC)

a(8)=98 was proven by: Östergård, P.R.J., Pettersson, V.H. Exhaustive Search for Snake-in-the-Box Codes. Graphs and Combinatorics 31, 1019–1028 (2015). https://doi.org/10.1007/s00373-014-1423-3

Zmatt (talk) 09:46, 7 August 2025 (UTC)

I suppose Randall doesn't consider beetles cute, or else philosophy of language would be included. 137.25.230.78 23:15, 6 August 2025 (UTC)

that's a great example 177.12.49.23 01:46, 7 August 2025 (UTC)

very nice one, reminds me of the story of the bug (moth) and debugging in computer science 88.129.22.189 (talk) 07:46, 1 September 2025 (please sign your comments with ~~~~)

In simultaneous interpreting, humans are the cute animal in the box. -- DrInterpreter (talk) 07:35, 7 August 2025 (UTC) (please sign your comments with ~~~~)

I don't believe an explanation of the Schrödinger's cat thought experiment is necessary to understand this comic. However, people keep editing the page to include an incorrect description of the experiment, by saying the cat is either dead or alive and you don't know which until you open the box. That's wrong and misses the point of quantum superposition. The cat is not dead or alive, it's literally both, due to its fate being linked to radioactive decay, a process that is subject to quantum superposition. Since it does seem inevitable that someone will keep editing this to add an explanation, I've added one myself. 177.12.49.23 10:29, 7 August 2025 (UTC)

The link in the mail newsletter lead to "http://https//xkcd.com/3125/", not sure if that's worth documenting here. Fabian42 (talk) 13:07, 7 August 2025 (UTC)

Not a chemistry grad student, but is it possible that Randall intended "lure campus squirrels into laundry hampers in the hope that it sparks inspiration" as a humorous method of investigating the triboelectric effect? 129.222.87.163 13:25, 7 August 2025 (UTC)

n=2: Snakes on a plane. 64.201.132.210 16:47, 7 August 2025 (UTC)

the comic number 3125 is 5^5 96.77.127.105 18:26, 7 August 2025 (UTC)

Conclusion: we better have no snakes in the world 102.117.215.0 (talk) 08:21, 8 August 2025 (UTC) (please sign your comments with ~~~~)

In the middle of the tree "wrong" examples, is the vertex leading from head to tail also a "wrong" vertex and should be coloured red? IIVQ (talk) 06:01, 9 August 2025 (UTC)

I suspect the squirrel fur + hamper + spark implies something electrochemical, though I haven't quite made the connection between the animal and the box. 88.129.22.189 (talk) 07:46, 1 September 2025 (please sign your comments with ~~~~)

I've found a length-373 snake in 10 dimensions. The previous record of 370 as listed on Wikipedia dates to 2012.

I started working on Snake-in-the-Box in August after xkcd #3125 introduced me to the problem. I'm grateful to Randall Munroe for calling it to my attention. I intend to keep working on it.

I described my results in a paper available at https://zenodo.org/records/17344872 which includes C code anyone can compile and run to validate the length-373 snake. doi:10.5281/zenodo.17344872

If you know anyone working in graph theory who can advise me on how to get my results recognized in a trusted forum (or who would even just like to compare notes about the Snake-in-the-Box problem), please let me know. My email address is in my paper.

Tom239 (talk) 19:46, 14 October 2025 (UTC)
        Add comment