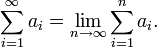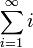2034: Equations
| Equations |
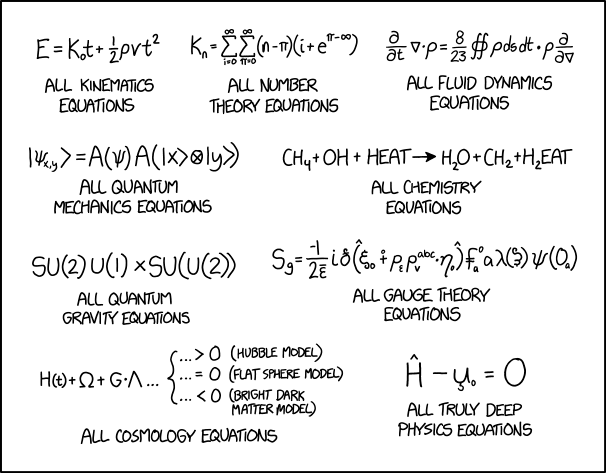 Title text: All electromagnetic equations: The same as all fluid dynamics equations, but with the 8 and 23 replaced with the permittivity and permeability of free space, respectively. |
Explanation
| |
This explanation may be incomplete or incorrect: TODO: some simplified explanations. Do NOT delete this tag too soon. If you can address this issue, please edit the page! Thanks. |
This comic gives a set of equations supposedly from different areas of science in mathematics, physics, and chemistry. To anyone not familiar with the field in question they look pretty similar to what you might find in research papers or on the relevant Wikipedia pages. To someone who knows even a little about the topic, they are clearly very wrong and only seem even worse the more you look at them. In many disciplines, the mathematical description of a large area is summed up in a small number of equations, such as Maxwell's equations for electromagnetism. In similar fashion, the equations here purport to encompass the whole of their given field.
Simplified Explanations
- All kinematics equations
Kinematics is the study of the motion of objects. More specifically, it describes how the location, velocity, and acceleration of an object vary over time. The equation shown contains two of these standard kinematic variables, velocity v and time t, in addition to several quantities (E, K0, and ρ) that are completely unrelated to kinematics.
- All number theory equations
Number theory is a branch of mathematics concerned primarily with the study of integers. However, the equation shown contains the non-integer Euler's constant e (approximately 2.718). It also uses the Greek letter π as an integer-valued variable, even though the symbol π is used in mathematics almost exclusively to denote the well-known non-integer circle constant (approximately 3.14159). Even with π treated as a variable here, one of its uses in the equation is still nonsensical. 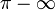 uses ∞ as if it were a specific number, which it is not, thus giving an undefined result.
uses ∞ as if it were a specific number, which it is not, thus giving an undefined result.
- All chemistry equations
Randall implies that all chemistry is just combustion of chemicals, demonstrated with an incorrect form of a common example chemistry equation of burning Methane and Oxygen (with added heat), to form water and carbon dioxide. However, in this form "HEAT" is an actual molecule, rather than simply indicating the presence of heat to start the reaction. Thus the equation is modified to incorporate the fictional "HEAT" into the reaction. While the H in "HEAT" is the chemical symbol of the element hydrogen, none of the letters E, A, or T are symbols of any actual elements. Also, to account for the second hydrogen in "H(2)EAT" on the products side, the oxygen gas on the reactants side has been altered to be hydroxide, a strong base that would not facilitate traditional combustion.
TODO: other simplified explanations.
Technical Explanations
- All kinematics equations
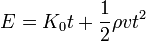
Kinematics describes the motion of objects without considering mass or forces. The latter is described by kinetics. The two fields get frequently confused due to the similarity of words.
This equation here literally states: "Energy equals a constant 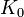 multiplied by time, plus half of density multiplied by speed multiplied by time squared".
multiplied by time, plus half of density multiplied by speed multiplied by time squared".
The first term here is hard to interpret: it could be correct if 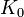 is a constant power applied to the system, but this symbol would more normally be used to denote an initial energy, in which case multiplying by
is a constant power applied to the system, but this symbol would more normally be used to denote an initial energy, in which case multiplying by 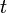 would be wrong. Alternatively, the term is similar to
would be wrong. Alternatively, the term is similar to 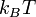 (sometimes written as kT), a term that often appears in statistical mechanics equations, where kB (or k) is the Boltzmann constant, and T is the absolute temperature. In this latter case, the term would have units of energy, consistent with the left side of the equation.
(sometimes written as kT), a term that often appears in statistical mechanics equations, where kB (or k) is the Boltzmann constant, and T is the absolute temperature. In this latter case, the term would have units of energy, consistent with the left side of the equation.
The second term looks similar to the kinetic energy term 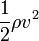 in the Bernoulli equation for fluids. (More properly, this is the kinetic energy density in the fluid).
in the Bernoulli equation for fluids. (More properly, this is the kinetic energy density in the fluid).
The whole equation appears to be a play on the kinematics formula: 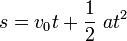 , where distance travelled (s) by a constantly accelerating object is determined by initial velocity (v0), time (t), and acceleration (a)
, where distance travelled (s) by a constantly accelerating object is determined by initial velocity (v0), time (t), and acceleration (a)
Kinematics is often one of the first topics covered in an introductory physics course, both at the high school and freshman college levels. As such, mixing in material from more advanced topics like statistical mechanics and the Bernoulli equation, even if done correctly, would be very confusing for a typical student learning kinematics.
- All number theory equations
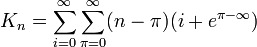
Number theory is a branch of mathematics primarily studying the properties of integers.
Said in English, the equation can be read: "The nth K-number is equal to the sum for all i from 0 to infinity of the sum for all π from 0 to infinity of n minus π, multiplied by i plus e raised to the power of π minus infinity." (i here is an iteration variable, not the imaginary number constant; e is Euler's number, approximately 2.718). A twofold misconception can be seen here. The first is the use of π as a variable instead of the circle constant (3.14...). This might be a jab at how in number theory letters and numbers are used interchangeably, but where some letters are suddenly fixed constants.
Further confusion comes from the use of unusual mathematical models. While the term 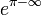 is meaningless when considered in standard ("high school") mathematics, it is valid when considered on the extended real number line, a concept unfamiliar to most non-mathematicians and uncommon in number theory. Naively, this would signify that (with the use of π as a variable) the exponent would range from negative infinity to zero. In fact, assuming e really does mean Euler's constant (or at least a real number strictly greater than 1) the term would be zero for every π < ∞. Ultimately, the sum diverges for every n.
is meaningless when considered in standard ("high school") mathematics, it is valid when considered on the extended real number line, a concept unfamiliar to most non-mathematicians and uncommon in number theory. Naively, this would signify that (with the use of π as a variable) the exponent would range from negative infinity to zero. In fact, assuming e really does mean Euler's constant (or at least a real number strictly greater than 1) the term would be zero for every π < ∞. Ultimately, the sum diverges for every n.
The close proximity of the letters i, e and π also evokes Euler's identity 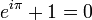 (also written
(also written 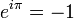 ), without actually using it, especially since both π and i are used as variables here.
), without actually using it, especially since both π and i are used as variables here.
- All fluid dynamics equations
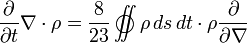
Fluid dynamics describes the movement of non-solid material. In particular for gases, the density 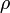 is often the most interesting quantity (for liquids, this is often just constant). A unique feature of fluid-dynamic equations is the presence of advection terms, which take the form of often strange-looking spatial derivatives. This equation turns this up to a new level by differentiating with respect to a differential operator
is often the most interesting quantity (for liquids, this is often just constant). A unique feature of fluid-dynamic equations is the presence of advection terms, which take the form of often strange-looking spatial derivatives. This equation turns this up to a new level by differentiating with respect to a differential operator  , which does not make any sense at all. Also it has a contour integral which seems reminiscent to a closed-circle process like in a piston engine, but this does not really fit in the context (differential description of a gas), and it has a pair of unexplained numbers
, which does not make any sense at all. Also it has a contour integral which seems reminiscent to a closed-circle process like in a piston engine, but this does not really fit in the context (differential description of a gas), and it has a pair of unexplained numbers 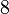 and
and 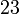 , probably alluding to the specific heat ratio which is often written out as the fraction
, probably alluding to the specific heat ratio which is often written out as the fraction 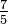 , whereas most other physics equations avoid including any plain numbers higher than 4.
, whereas most other physics equations avoid including any plain numbers higher than 4.
The title text stating that the electromagnetism equation is the same as the fluid dynamics equation, but with the arbitrary 8 and 23 replaced with the permittivity and permeability of free space is likely because electromagnetism equations often have relations to fluid dynamics, and because those two constants appear in the vast majority of electromagnetism equations.
- All quantum mechanics equations
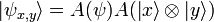
Quantum mechanics is a fundamental theory in physics which describes nature at scales of atoms and below. It typically uses the bra–ket notation in its formulae.
This equation takes a state psi in the dimensions of x and y and equates it to an operator A performed on psi multiplied by the same operator performed on the tensor product of x and y. Since the state psi is already the tensor product of the states x and y, this is equivalent to performing the same unknown operator twice on psi, and unless this operator is the identity or is its own inverse such as a bit-flip or Hermitian operator, this equation is therefore incorrect.
- All chemistry equations
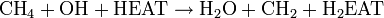
A chemical equation represents a chemical reaction as a formula, with the reactant entities on the left-hand side, and the product entities on the right-hand side. The number of each element on the left side must match those on the right side. The energy produced or absorbed in this process is not included in that formula.
This is a modification of the combustion of methane. The correct form is often taught and a good example problem but obviously there are more chemistry problems.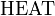 is normally shorthand for activation energy, but in Randall's version it's jokingly used as a chemical ingredient and becomes
is normally shorthand for activation energy, but in Randall's version it's jokingly used as a chemical ingredient and becomes 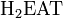 , taking the hydrogen atom freed by the combustion equation shown. The proper methane combustion equation would be:
, taking the hydrogen atom freed by the combustion equation shown. The proper methane combustion equation would be: 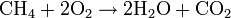
While 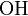 often appears in chemical equations in the form of a negatively charged hydroxide group (
often appears in chemical equations in the form of a negatively charged hydroxide group (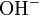 ), the left side of the equation involves a bare
), the left side of the equation involves a bare 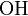 , possibly the highly unstable hydroxyl radical (although this would typically be written with a leading dot, e.g.
, possibly the highly unstable hydroxyl radical (although this would typically be written with a leading dot, e.g. 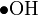 ). Similarly, the right side contains an unstable methylene radical which would generally only appear as an intermediate rather than a product.
). Similarly, the right side contains an unstable methylene radical which would generally only appear as an intermediate rather than a product.
- All quantum gravity equations
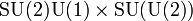
This is more similar to expressions which appear in Grand Unified Theory (GUT) than general quantum gravity. Unlike some of the other equations, this one has no interpretation which could make it mathematically correct. This is similar to the notations used to describe the symmetry group of a particular phenomena in terms of mathematical Lie Groups. A real example would be the Standard Model of particle physics which has symmetry according to 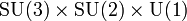 . Here,
. Here, 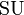 and
and 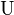 denote the special unitary and unitary groups respectively with the numbers indicating the dimension of the group. Loosely, the three terms correspond to the symmetries of the strong force, weak force and electromagnetism although the exact correspondence is muddied by symmetry breaking and the Higgs mechanism.
denote the special unitary and unitary groups respectively with the numbers indicating the dimension of the group. Loosely, the three terms correspond to the symmetries of the strong force, weak force and electromagnetism although the exact correspondence is muddied by symmetry breaking and the Higgs mechanism.
Of course, an expression missing an "=" sign, is difficult to interpret as an "equation", because equations normally express an "equality" of some kind. Nobody knows whether Randal refers to a horse, zebra, donkey or other equine here.
Randall's version clearly involves some similar groups although without the 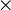 symbol it is hard to work out what might be happening. A term like
symbol it is hard to work out what might be happening. A term like 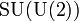 has no current interpretation in mathematics, if anyone thinks otherwise and possibly has a solution to the quantum gravity problem they should probably get in touch with someone about that.
has no current interpretation in mathematics, if anyone thinks otherwise and possibly has a solution to the quantum gravity problem they should probably get in touch with someone about that.
In physics, a gauge theory is a type of field theory which is invariant to local transformations. The term gauge refers to any specific mathematical formalism to regulate redundant degrees of freedom.
This equation looks broadly similar to the sorts of things which appear in gauge theory such as the equations which define Yang-Mills Theory. By the time physics has got this far in, people have normally run out of regular symbols making a lot of the equations look very daunting. The actual equations in this field rarely go far beyond the Greek alphabet though and no-one has yet to try putting hats on brackets. The appearance of many sub- and superscripts is normal (this links to the group theory origins of these equations) and for the layperson it can be impossible to determine which additions are labels on the symbols and which are indices for an Einstein Sum.
The left-hand side 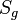 is the symbol for some action, in Yang-Mills theory this is actually used for a so-called "ghost action". On the right-hand side we have a large number of terms, most of which are hard to interpret without knowing Randall's thought processes (this is why real research papers should all label their equations thoroughly). The
is the symbol for some action, in Yang-Mills theory this is actually used for a so-called "ghost action". On the right-hand side we have a large number of terms, most of which are hard to interpret without knowing Randall's thought processes (this is why real research papers should all label their equations thoroughly). The 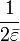 looks like a constant of proportionality which often appears in gauge theories. The factor of
looks like a constant of proportionality which often appears in gauge theories. The factor of  is not unusual as many of these equations use complex numbers. The
is not unusual as many of these equations use complex numbers. The 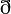 symbol looks similar to a
symbol looks similar to a 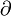 partial derivative symbol especially as the Dirac Equation uses a slashed version as a convenient shorthand.
partial derivative symbol especially as the Dirac Equation uses a slashed version as a convenient shorthand.
The rest of the equation cannot be mathematically correct as the choice of indices used does not match that on the left-hand side (which has none). In particle physics subscripts (or superscripts) of greek letters (usually 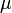 or
or 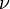 ) indicate terms which transform nicely under Lorentz transformations (special relativity). Roman indices from the beginning of the alphabet relate to various gauge transformation propetries, the triple index seen on
) indicate terms which transform nicely under Lorentz transformations (special relativity). Roman indices from the beginning of the alphabet relate to various gauge transformation propetries, the triple index seen on 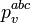 would likely come from some
would likely come from some 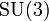 transformation (related to the strong nuclear force). Since
transformation (related to the strong nuclear force). Since 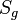 has none of these (and is thus a scalar which remains constant under these operations), we would need the right-hand side to behave in the same way. Most of the indices which appear are unpaired and so will not result in a scalar making the equation very wrong. For those not familiar with this type of equation, this is similar to the mistake of messing up units, for instance setting a distance equal to a mass.
has none of these (and is thus a scalar which remains constant under these operations), we would need the right-hand side to behave in the same way. Most of the indices which appear are unpaired and so will not result in a scalar making the equation very wrong. For those not familiar with this type of equation, this is similar to the mistake of messing up units, for instance setting a distance equal to a mass.
- All cosmology equations
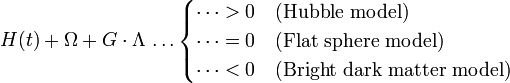
This is a parody of equations defining the Hubble Parameter 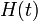 although it looks like Randall has become bored and not bothered to finish his equation. Such equations usually have several
although it looks like Randall has become bored and not bothered to finish his equation. Such equations usually have several 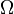 terms representing the contributions of different substances to the energy-density of the Universe (matter, radiation, dark energy etc.). In this context
terms representing the contributions of different substances to the energy-density of the Universe (matter, radiation, dark energy etc.). In this context 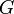 could be Newton's constant and
could be Newton's constant and 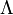 is the cosmological constant (energy density of empty space) although seeing them appear multiplied and on the same footing as
is the cosmological constant (energy density of empty space) although seeing them appear multiplied and on the same footing as 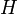 is unusual (the dot is entirely unnecessary). Choosing to make
is unusual (the dot is entirely unnecessary). Choosing to make 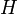 a function of time
a function of time 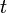 and not of redshift
and not of redshift 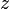 is also unusual.
is also unusual.
The second section looks like the inequalities used to show how the equation varies with the shape of the Universe, based on the value of the curvature parameter 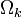 . A value of 0 indicates a flat Universe (this is more or less what we observe) while a positive /negative value indicates an open /closed curved Universe. Randall's choice of labels further makes fun of the field as both a flat sphere and bright dark matter are oxymoronic terms which would involve some rather strange model universes.
. A value of 0 indicates a flat Universe (this is more or less what we observe) while a positive /negative value indicates an open /closed curved Universe. Randall's choice of labels further makes fun of the field as both a flat sphere and bright dark matter are oxymoronic terms which would involve some rather strange model universes.
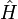 is the Hamiltonian operator, which when applied to a system returns the total energy. In this context, U would usually be the potential energy. However, there is also a subscript 0 and a diacritic marking indicating some other variable. Much of physics is based on Lagrangian and Hamiltonian mechanics. The Lagrangian is defined as
is the Hamiltonian operator, which when applied to a system returns the total energy. In this context, U would usually be the potential energy. However, there is also a subscript 0 and a diacritic marking indicating some other variable. Much of physics is based on Lagrangian and Hamiltonian mechanics. The Lagrangian is defined as 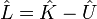 with K being the kinetic energy and U the potential. Hamiltonian mechanics uses the equation
with K being the kinetic energy and U the potential. Hamiltonian mechanics uses the equation 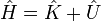 . The Hamiltonian must be conserved so taking the time derivative and setting it equal to zero is a powerful tool. The "principle of least action" allows most modern physics to be derived by setting the time derivative of the Lagrangian to zero.
. The Hamiltonian must be conserved so taking the time derivative and setting it equal to zero is a powerful tool. The "principle of least action" allows most modern physics to be derived by setting the time derivative of the Lagrangian to zero.
Transcript
- [Nine equations are listed, three in the top row and two in each of the next three rows. Below each equation there are labels:]
- E = K0t + 1/2 ρvt2
- All kinematics equations
- Kn = ∑i=0∞∑π=0∞(n-π)(i-eπ-∞)
- All number theory equations
- ∂/∂t ∇ ⋅ ρ = 8/23 (∯ ρ ds dt ⋅ ρ ∂/∂∇)
- All fluid dynamics equations
- |ψx,y〉 = A(ψ) A(|x〉⊗ |y〉)
- All quantum mechanics equations
- CH4 + OH + HEAT → H2O + CH2 + H2EAT
- All chemistry equations
- SU(2)U(1) × SU(U(2))
- All quantum gravity equations
- Sg = (-1)/(2ε̄) i ð (̂ ξ0 +̊ pε ρvabc η0 )̂ f̵a0 λ(ʒ̆) ψ(0a)
- All gauge theory equations
- [There is a brace linking the three cases together.]
- H(t) + Ω + G⋅Λ ...
- ... > 0 (Hubble model)
- ... = 0 (Flat sphere model)
- ... < 0 (Bright dark matter model)
- All cosmology equations
- Ĥ - u̧0 = 0
- All truly deep physics equations
Discussion
Is the joke that all of the equations are actually wrong/malformed/meaningless but they sort of look like typical equations for that field? 172.68.133.66 (talk) (please sign your comments with ~~~~)
- Sort of. A bit of dimensional analysis would have helped. ;-) --162.158.91.221 07:28, 17 August 2018 (UTC)
- I feel that the joke is that all the equations are very complicated, and use multiple letters and symbols. But the last one "Truly deep Physics Equations" are summed up with just 3 characters and 2 basic operators. 108.162.250.11 10:56, 19 August 2018 (UTC)
He's nerd sniping us all.. (162.158.167.120 03:30, 18 August 2018 (UTC))
- ..and perhaps forcing us to build out symbolic usage which is not generating well for math parsers, wiki, etc. 162.158.186.60 14:45, 21 August 2018 (UTC)
Should we add a column with examples of similar correct equations from the respective fields? Sebastian --172.68.110.4 09:33, 17 August 2018 (UTC)
- That would definitely tidy up my attempts to provide context for Randall's versions. The challenge then is working in explanations for the correct equations as well as arguing over which examples should be used. Exxi (talk) 09:45, 17 August 2018 (UTC)
I don't think the part in parentheses about OH in the Chemistry equation explanation is correct. OH- would mean that it's negatively charged and has nothing to do with unpaired electrons of Oxygen. It would add another horror to the equation, though, as it wouldn't be charge preserving anymore. 162.158.88.230 09:58, 17 August 2018 (UTC)
"Redshit". Best typo ever. Please keep it. 172.69.54.177 10:13, 17 August 2018 (UTC)
- Deep physics equations
The transcript is wrong here, the last letter is not a  , but a "u" with a cedilla: u̧. The math parser refuses to render it, though. 162.158.88.230 05:54, 17 August 2018 (UTC)
, but a "u" with a cedilla: u̧. The math parser refuses to render it, though. 162.158.88.230 05:54, 17 August 2018 (UTC)
- Looks like it. But I don't think that letter exists even. --162.158.91.221 07:28, 17 August 2018 (UTC)
- Is this equation a sort of nod to a Theory Of Everything which unifies quantum mechanics and gravity... H-hat (a Hamiltonian, which in quantum mechanics describes the total energy of a system, and usually runs in to problems describing large systems - such as the entire universe - where gravity or spacetime curvature effects matter) *minus* u0 (the relativistic mass of the whole system at time zero ie. the big bang) gives 0 (no energy everywhere always). Since mass is energy (e=mc^2) and mass is also the sole cause of gravity the two theories cleanly collapse together when mass is zero, and figuring out how to extend the theory to other less clean points on the mass axis is obviously a job for less profound physics? I've no ideas to explain the cedilla. 141.101.98.28 08:49, 17 August 2018 (UTC)
- It looks to me a little like a parody of the Wheeler-DeWitt equation which (in theory) describes a wavefunction for the entire Universe. Exxi (talk) 09:06, 17 August 2018 (UTC)一
- I'm just thrilled someone found the right character for it. I spent 20 minutes looking for the right u symbol without any luck at all. 172.68.143.132 (talk) (please sign your comments with ~~~~)
Is this poking fun at equation-filled blackboards in movies and cartoons? 172.68.254.42 (talk) (please sign your comments with ~~~~)
- Doesn't seem like it. These equations actually do look like the kinds of equations you would see in these fields. On blackboards in movies you tend to get equations that are pure nonsense. 172.68.143.132 (talk) (please sign your comments with ~~~~)
I think this may also be a reference to Feynman's unworldliness equation, http://www.feynmanlectures.caltech.edu/II_25.html#Ch25-S6 . 108.162.219.220 17:02, 17 August 2018 (UTC)
I'd thought the point of the "u" with the cedilla was simply visual (not a reference to an actual parameter). It visually looks like the head of "The Thinker" in profile with the bottom of the "u" being the chin and the cedilla being the curled hand upon which the chin rests. So, the joke would be a twist on the term "deep" where in the cartoon the u+cedilla represents deep thought rather than far away (deep) into space. Monroe likes these little visual puns.Genejockey33000 (talk) 14:01, 22 August 2018 (UTC)
I don't like the comparison with 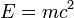 . 'Deep' physics equations have a lot of meaning assigned to each symbol, with each prime, tilde or cedilla adding meaning, and with complicated operations implicit (Think operators, tensor products etc.). Einstein's relation is just a relation between 3 scalar variables, with the only operation being multiplication. I appreciate not wanting to get too complicated. Can we do any better? I can't help thinking that writing down the GFEs in natural units and saying 'this describes all of spacetime' owtte would be just as effective and more accurate...Jezza2 (talk) 16:03, 24 January 2019 (UTC)
. 'Deep' physics equations have a lot of meaning assigned to each symbol, with each prime, tilde or cedilla adding meaning, and with complicated operations implicit (Think operators, tensor products etc.). Einstein's relation is just a relation between 3 scalar variables, with the only operation being multiplication. I appreciate not wanting to get too complicated. Can we do any better? I can't help thinking that writing down the GFEs in natural units and saying 'this describes all of spacetime' owtte would be just as effective and more accurate...Jezza2 (talk) 16:03, 24 January 2019 (UTC)
- Table layout at the explanation
That oversized table is really bad layout. We've had this discussion many times before - tables should only be used for small contents. Right now I would run into too many edit conflicts but I'll change it to a proper floating text with small headers for each section. --Dgbrt (talk) 11:51, 17 August 2018 (UTC)
- All number theory equation
The explanation for math doesn't seem entirely correct. You can in fact extend the ring of integers (as well as rational and real numbers) with positive and negative infinity, but it won't be a ring anymore. Specifically, the infinities don't have an additive or multiplicative inverse (but 1/infinity = 0); and addition of positive and negative infinity, as well as the product of 0 and either infinity is undefined. However, these properties are not used in the above equation. What we can use is that 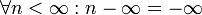 . We would thus have
. We would thus have 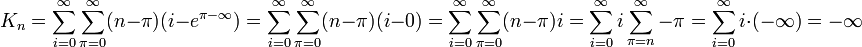 . Also, how often does one use e and pi in number theory? --Ycthiognass (talk) 12:11, 17 August 2018 (UTC)
. Also, how often does one use e and pi in number theory? --Ycthiognass (talk) 12:11, 17 August 2018 (UTC)
- Pi (or any other number) minus infinite is just absurd. You can use the infinite symbol only as a limit but NOT as number in calculations. --Dgbrt (talk) 12:33, 17 August 2018 (UTC)
- It is not absurd. Adding the rules
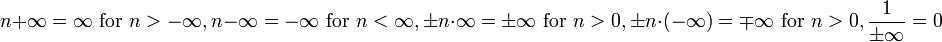 gives you a consistent theory that is especially useful when talking about infinite sums and integrals. Would you say the term
gives you a consistent theory that is especially useful when talking about infinite sums and integrals. Would you say the term 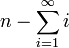 is absurd? --Ycthiognass (talk) 14:35, 17 August 2018 (UTC)
is absurd? --Ycthiognass (talk) 14:35, 17 August 2018 (UTC)
- Of course it's absurd. It is
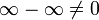 because it could be everything between
because it could be everything between 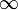 and
and 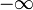 . Infinity is a concept describing something without any bound... And, as you can't divide by zero you can't do the same for infinity. --Dgbrt (talk) 17:24, 17 August 2018 (UTC)
. Infinity is a concept describing something without any bound... And, as you can't divide by zero you can't do the same for infinity. --Dgbrt (talk) 17:24, 17 August 2018 (UTC) - One more: It is
- When this limit exists, one says that the series is convergent or summable. Otherwise it's called divergent and has no solution like this one:
- Infinite is NO number! --Dgbrt (talk) 17:33, 17 August 2018 (UTC)
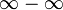 is indeterminate, just like 0/0 is in standard arithmetic. That's cool, because we don't need the value of
is indeterminate, just like 0/0 is in standard arithmetic. That's cool, because we don't need the value of 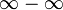 to calculate the above expression. Have a look at the extended real number line. --Ycthiognass (talk) 06:18, 20 August 2018 (UTC)
to calculate the above expression. Have a look at the extended real number line. --Ycthiognass (talk) 06:18, 20 August 2018 (UTC)
- Of course it's absurd. It is
- It is not absurd. Adding the rules
- Number theorists use
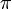 and
and  very often indeed, especially analytic number theorists (and since the double sum at hand is infinite it seems entirely fair to consider it analytic number theory territory). The exponential function
very often indeed, especially analytic number theorists (and since the double sum at hand is infinite it seems entirely fair to consider it analytic number theory territory). The exponential function 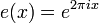 is used all over in this field because of Fourier series (the coefficients of which, it turns out, can give remarkable amounts of arithmetic information if used properly).
is used all over in this field because of Fourier series (the coefficients of which, it turns out, can give remarkable amounts of arithmetic information if used properly). - The same field of analytic number theory uses the infinity symbol
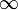 in calculations quite frequently too, because it is not uncommon to work on the Riemann sphere, which is the complex plane with a "point at infinity added". (That said, it doesn't quite save our hides in this particular comic, because the point at infinity doesn't have an additive inverse in this context.)
in calculations quite frequently too, because it is not uncommon to work on the Riemann sphere, which is the complex plane with a "point at infinity added". (That said, it doesn't quite save our hides in this particular comic, because the point at infinity doesn't have an additive inverse in this context.) - For the record there are also numerous ways to extend the real numbers to include infinities in more or less algebraically nice ways, ranging from compactifying it by just tacking a point at infinity on (as with the Riemann sphere for the complex numbers, also called a projective extension), tacking a positive and negative infinity on as with the extended real line as above, to more algebraically nice structures like the hyperreals and surreals which are full blown fields. In these latter constructions it is not customary to use the
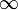 symbol, however, because there is more than just the one infinity in both, but they do allow us to make meaningful and useful sense of things like "infinity - infinity". Prstq (talk)
symbol, however, because there is more than just the one infinity in both, but they do allow us to make meaningful and useful sense of things like "infinity - infinity". Prstq (talk)
Completely separate from the above, it's probably worth noting that i is also a constant, and as such has the same misconception as 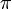 . Computer scientists are happy using i for loops/summations, but mathematicians prefer using n. Based off that, it's probably another misconception/joke that n is treated as a constant, while known-constants are used as variables. 108.162.246.149 17:28, 17 August 2018 (UTC)
. Computer scientists are happy using i for loops/summations, but mathematicians prefer using n. Based off that, it's probably another misconception/joke that n is treated as a constant, while known-constants are used as variables. 108.162.246.149 17:28, 17 August 2018 (UTC)
- There is nothing non-standard about using i as an index variable. Often as part of the series i,j,k. Searching for summation convention will give plenty of examples.
- There are fewer letters than mathematical concepts in need of letters, so most letters are used for multiple purposes. Occasionally this causes difficulty. You can be halfway through a linear algebra problem before you discover you need i for an imaginary number despite already using it as an index. Hilarity ensues. 162.158.74.105 19:57, 17 August 2018 (UTC)
Is it worth mentioning Euler's identity in the explanation? As a non-mathematician, the presence of e, pi, and i together in one equation looks "Euler's identity-ish" while clearly not being it. 162.158.74.39 22:20, 19 August 2018 (UTC)
Honestly, seeing e, pi, and i isn't that farfetched, since quite a few applications of number theory to coordinate systems (in the computer-ey sense) take familiar XY coordinates, make them polar, and call them to complex numbers, with a bunch of operations done by multiplying by e to some complex power or other. And wherever waves go, pi goes... Coming from nothing more than a high-school background, this whole system can be rather jarring, and difficult to understand. I'm just glad I understand enough bits and pieces of number theory to laugh at Randall's joke. 162.158.186.12 19:41, 1 September 2018 (UTC)
- Chemistry equation
OH should have a charge symbol: OH-. The actual reaction would be:
CH4 + OH- + heat -> CH3- + H2O
The methyl group can dissolve in water, and this is presumably happening in water, so this equation can work, just not the one provided by Randell. Reacting longer alkanes with bases is a way to make soaps, but the methyl group would be too reactive to be used this way. Nutster (talk) 13:13, 17 August 2018 (UTC) OH without any charge is the hydroxil radical, a highly reactive moleculte, that in fact abstracts H (hydrogen atom, not a proton) from hydrocarbons. This is one step of combustion processes. The methyl radical generated combines itself quickly with oxygen. The hydroxide anion you propose OH- do not react with hydrocarbons.
- Fluid Dynamics equation
I believe the fraction 8/23 in the Fluid Dynamics equation is a Randallesque reference to the fractional approximation of pi = 22/7. It's probably not a coincidence that you get 8/23 from 22/7 if you invert it and add 1 to both the numerator and denominator. Ianrbibtitlht (talk) 15:19, 17 August 2018 (UTC)
- I think that is a bit of a stretch. If Randall wanted to reference the 22/7 approximation, I think he would simply use 22/7 and not 8/23. Redbelly98 (talk) 00:40, 18 August 2018 (UTC)
- It might be a stretch, but maybe Randall wanted to be more clever than just inserting 22/7, since pi really has no place in that equation. I don't see anyone else suggesting any reasonable source for 8/23 in the equation. The current explanation is an even bigger stretch, since it has nothing in common with 8/23 beyond being just another fraction - it seems to suggest he picked two random numbers, 8 and 23, for the fraction! How unsatisfying! But if nobody else agrees, I'm not losing any sleep over it. (Sometimes I wish Randall would chime in to clear things like this up for us. Randall, where are you?) Ianrbibtitlht (talk) 04:54, 18 August 2018 (UTC)
- Fluid dynamicist here -- strange looking numbers and fractions come from multiplying tensors. 2/3 is a common one, but you also get numbers like 1/7 and 8/27.108.162.241.166 07:24, 18 August 2018 (UTC)
I changed a "p" to a Greek "rho". Redbelly98 (talk) 00:40, 18 August 2018 (UTC)
The 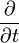 is the partial derivative of a function. The ∇ symbol (Nabla) denotes the vector of all partial derivatives of a function (called its gradient; eg. ∇(x+2y²)=(1,4y) ); ∇⋅ is the curl operator. 162.158.91.59 18:53, 5 December 2018 (UTC)
is the partial derivative of a function. The ∇ symbol (Nabla) denotes the vector of all partial derivatives of a function (called its gradient; eg. ∇(x+2y²)=(1,4y) ); ∇⋅ is the curl operator. 162.158.91.59 18:53, 5 December 2018 (UTC)
- Gauge theory equation
I think the transcript is missing a left superscript 0 before the turned xi. 172.68.226.16 16:50, 17 August 2018 (UTC) Ah no, sorry. False alarm. It's just that Randall writes the xi with a funny tail. The same tail is on the non-turned xi earlier. 172.68.226.10 16:52, 17 August 2018 (UTC)
If explainxkcd.com is to make XKCD comics more understandable then this explanation is failing that. I assumed from the beginning that the joke was about the equations being wrong, but the description of the joke is making my head hurt. 162.158.106.216 (talk) (please sign your comments with ~~~~)
- Read the first paragraph: "To someone who knows even a little about the topic, they are clearly very wrong and only seem even worse the more you look at them." Nevertheless the rest sometimes does hurt. See below. --Dgbrt (talk) 20:28, 17 August 2018 (UTC)
- All truly deep physics equations
In the description paragraph, the last sentence starting "The principle of least action says allows..." does not scan. If someone can fix this (copy&paste?) error, please delete this comment. 162.158.58.171 19:33, 17 August 2018 (UTC)
- I edited the sentence slightly to address this issue. Ianrbibtitlht (talk) 20:51, 17 August 2018 (UTC)
It looks like there is already a section for this above, "Deep physics equations", or am I missing something? Redbelly98 (talk) 00:40, 18 August 2018 (UTC)
Note that this comics also emphasizes that Randall is more familiar with physics than with chemistry : while most of the equations here require college-level education to grok, the chemistry one is at the very most high-scool-grade. 141.101.69.33 (talk) (please sign your comments with ~~~~)
Could this be a reference to Feynman's jab at hiding complexity underneath symbol definitions to achieve 'simplicity'? See the Feynman Lectures on Physics, Volume II, Chapter 25, Section 6. 162.158.150.100 09:19, 19 August 2018 (UTC)WhoIsJack
- Explanations in general
“Nobody knows if Randall references a horse here” - what?! Because the expression lacks an equal sign; doesn’t represent an equality, it might mean Randall is referencing equines, aka horses?! Is this vandalism, an attempt at a joke, or what? This explanation clearly still needs quite a bit of work! PotatoGod (talk) 20:14, 17 August 2018 (UTC)
- I've put a header on top here. It's not vandalism but every explanation looks still highly unscientific. I've gave real sources to the most topics at the beginning but the following explanations are mostly bad. --Dgbrt (talk) 20:22, 17 August 2018 (UTC)
- I left that joke in as it was added whilst I was editing the rest of it, I don't think it belongs though. I did my best to reference real-life stuff while writing [Gauge, Quantum Gravity and Cosmology] the awfulness of the equations makes it hard to be scientific though. If there are specific issues I can have a shot at improving those sections although it's kinda hard to explain why I find them funny without going deep into the related physics. I'm not convinced it's possible to properly get that across to a non-physicist in a paragraph of explainXKCD. Exxi (talk) 19:29, 23 August 2018 (UTC)
- Kinematics equations
I fixed an error: Randall's Greek "rho" ρ, a common symbol for mass density, was incorrectly shown here as p, the common symbol for momentum. The term with the ρ is very similar to a term in the Bernoulli equation, and I have changed the explanation to reflect this. Redbelly98 (talk) 00:40, 18 August 2018 (UTC)
It seems pretty clear to me that this equation is a mash-up of physical kinematics with Michaelis-Menten kinetics (enzyme kinetics). Those equations use both velocity (of reaction) and K (KM) as well as subscripts (e.g. v0, vmax); and while density is commonly not included it's not quite as out-of-the-blue for this field as it is in "regular" kinematics. Rebecka (talk) 06:46, 3 January 2022 (UTC)
- You might be overthinking some of these
For example, I see the first one as Energy = cot + private which would be an Army private resting in a cot to regain their energy. The second one I see the word Knee, so I'm thinking it's either something about taking an arrow to a knee, or perhaps about the Knights of Ki who regain their power by saying "Ni!" The fourth one, I see most of the word ANALOGY, so perhaps the trident-shaped thing equals N, and x> = L, and l (or 1) = G, so if you resolve all the way through you get GNL = ANALOGY and I don't have that quite right yet. SU(2)U(1)xSU(U(2)) makes me think of Phil Collins singing "Su-Su-Sussudio oh oh". --108.162.245.40 20:37, 18 August 2018 (UTC)
- Has anyone considered the joke part?
As someone unfamiliar with scientific equations, I took the joke to be that Scientific Equations Are Complicated, until you get to the "truly deep" part, in which case they're pretty simple. As much as I appreciate the description of the equations, is anyone gonna explain whether my take on the joke is plausible? Or what it is if I'm wrong? 108.162.219.214 15:52, 20 August 2018 (UTC)
- Is there a pun?
Am I the only one seeing a possible pun in SU(2)U(1)xSU(U(2))? I can't figure out the whole thing but SU(U(2)) sure looks like it reads "sue you too". 24.165.207.66 23:02, 20 August 2018 (UTC)
- No element symbols exist to form EAT
Although you could write HeAt (Helium-Astatine), I could find no element symbols to form EAT on the right-hand side of the reaction, so it appears to be an invalid expression anyway. (and yes, of course I know Randall is messing with us and you might be expected to read the first "heat" as "temperarature".) --IByte (talk) 11:17, 4 September 2018 (UTC)
- And Randall wrote HEAT, not HeAt. They are different. Redbelly98 (talk) 18:33, 9 September 2018 (UTC)
- Heat (Q) is not interchangeabil with temperature (T). EAT could mean element-acid group-tritium or obsoletely erbium-argon-tritium. Lysdexia (talk) 01:42, 5 January 2019 (UTC)
Why does the notice still say 2034 lacks a complete explanation when here's no incomplete template? Lysdexia (talk) 01:42, 5 January 2019 (UTC)
- Missing alt-text 141.101.77.104 12:19, 19 January 2019 (UTC)